Алфавит языка описания формул

Основные символы языка описания формул это - буквы, цифры и специальные символы: 26 прописных и строчных латинских букв: A, …, Z, a, …, z 10 цифр: 0, …, 9 знаки операций: + - * / ^ знаки условных операций: = < > <= <= <> ограничители и разделители: , ( ) | ; … ключевые (зарезервированные) слова: if then else and or begin end

<Аргумент функции>

::= <Выражение>{, <Выражение>} | {<Выражение>,}<Перечисление аргументов>{,<Выражение>}

<Аргумент локальной функции>

::= U

Примечание: <Аргумент локальной функции> можно использовать только в <Описании локальной функции>

<Буква>

::= А|В|С|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z| a|b|c|d|e|f|g|h|i|j|k|l|m|n|o|p|q|r|s|t|u|v|w|x|y|z

<Число>

::= <Целое число> | <Вещественное число>

<Дополнительная переменная>

::= <Буква>{<Буква>}[<Целое число>]

Примечание: Значение <Дополнительной переменной> не может принимать значения зарезервированные за <Переменной цикла>, <Аргументом локальной функции>, <Результатом> и <Ключевым словом>

<Формула>

::= {<Определение локальной функции> | <Определение>} <Результирующие определение>

<Функция>

::= <Имя функции> "("<Аргумент функции>")"

Примечание: У некоторых <Функций> (например, SUM или PROD) аргументы анализируются особым образом

Грамматика языка описания формул

Язык описания математических формул можно задать более формально с использованием грамматики в расширенной форме Бэкуса-Наура с использованием следующих соглашений: символ "::=" отделяет левую часть правила от правой; нетерминалы обозначаются словами (написанными на русском языке), выражающими их интуитивный смысл, заключаются в угловые скобки "<" и ">"; терминалы - это символы, используемые в описываемом языке; каждое правило определяет порождение нескольких альтернативных цепочек, отделяемых друг от друга символом вертикальной черты "|"; квадратные скобки "[" и "]" означают, что заключенная в них синтаксическая конструкция может отсутствовать; фигурные скобки "{" и "}" означают, что заключенная в них синтаксическая конструкция может повторяться (возможно, ноль раз); сочетание фигурных скобок и косой черты "{/" и "/}" используется для обозначения повторения один и более раз; круглые скобки "(" и ")" используются для ограничения альтернативных конструкций; в кавычках " " заключаются символы: "< > ( ) |", если они используются в качестве терминалов. правила не чувствительны к регистру символов к некоторым правилам идут примечания, описывающие их особенности, которые нельзя формализовать

Язык описания математических формул

В качестве формулы выступает функция многих переменных F(x), x=(x1,…, xn).

Элементарные конструкции

Элементарные конструкции языка описания формул включают в себя идентификаторы и числа. Идентификаторами называют элементы языка: переменные, функции и константы. Идентификатор это последовательность букв и чисел, начинающаяся с буквы. Идентификаторы не чувствительны к регистру букв. Запрещается использовать в качестве идентификаторов ключевые слова.

<Ключевое слово>

::= IF | THEN | ELSE | NOT | AND | OR | BEGIN | END

Комментарии представляют

Комментарии представляют собой текстовые строки, предназначенные для аннотирования формулы. В языке описания формул поддерживается два типа комментариев: однострочные и многострочные. Первый тип начинается с последовательности "//" и при этом комментируется весь текст после нее до конца строки. Второй тип комментария может быть использован для выделения в комментарий многострочного текста, его начало и конец обозначаются соответственно "{" и "}" или " (*" и "*)", весь текст размещенный между этими символами, считается комментарием.

<Комментарий>

::== "//" <Любой текст> <Перевод строки>| "{"{<Любой текст> [<Перевод строки>]}"}" "(*"<Любой текст> [<Перевод строки>] "*)"

Примечание: Все <Комментарии> в процессе анализа пропускаются

<Константа>

::= PI | DIM

Примечание: <Константа> DIM описывает размерность вектора входящих переменных

Литература

Скачать "Библиотеку для разбора и трансляции математических формул: optMathParser": (177K)
Примечание к архиву:
Для того что бы скомпилировать этот проект в настройках проекта надо прописать SearchPath до папок:
kaOptima
MathExprDraw
QStrings Не ВСЕ файлы присутствуют в виде исходных текстов, то что я считаю своим "know-how" присутствует в виде *.dcu (Delphi 7) Эта библиотека является частью пакета глобальной поисковой непараметрической оптимизации kaOptima и успешно используется в течении 3-х лет В качестве некоторой документации по библиотеке см. папку Doc, в которой находится интерфейсная часть модуля optMathParser. Библиотека QStrings: Copyright (C) 2000, 2001
Portions (C) 2000, Библиотека MathExprDraw: и некоторые модификации внесены - мной, в тексте помечены {kuaw} document.write('');

Новости мира IT: 02.08 - 02.08 - 02.08 - 02.08 - 02.08 - 01.08 - 01.08 - 01.08 - 01.08 - 01.08 - 01.08 - 01.08 - 01.08 - 01.08 - 01.08 - 31.07 - 31.07 - 31.07 - 31.07 - 31.07 -

Архив новостей

Последние комментарии: (66)
2 Август, 17:53 (19)
2 Август, 17:51 (34)
2 Август, 15:40 (42)
2 Август, 15:35 (1)
2 Август, 14:54 (3)
2 Август, 14:34 (3)
2 Август, 14:15 (2)
2 Август, 13:34 (7)
2 Август, 13:04 (3)
2 Август, 12:28 BrainBoard.ru
Море работы для программистов, сисадминов, вебмастеров.
Иди и выбирай! Loading google.load('search', '1', {language : 'ru'}); google.setOnLoadCallback(function() { var customSearchControl = new google.search.CustomSearchControl('018117224161927867877:xbac02ystjy'); customSearchControl.setResultSetSize(google.search.Search.FILTERED_CSE_RESULTSET); customSearchControl.draw('cse'); }, true);

IT-консалтинг

Software Engineering

Программирование

СУБД

Безопасность

Internet

Сети

Операционные системы

Hardware

PR-акции, размещение рекламы — ,
тел. +7 495 6608306, ICQ 232284597

Пресс-релизы —

This Web server launched on February 24, 1997
Copyright © 1997-2000 CIT, © 2001-2009

Внимание! Любой из материалов, опубликованных на этом сервере, не может быть воспроизведен в какой бы то ни было форме и какими бы то ни было средствами без письменного разрешения владельцев авторских прав.

Интересно: на www.td-vessel.ru.

<Локальная функция>

::= <Имя локальной функция>"("<Аргумент функции>")"

<Операция сравнения>

::= = | "<" | ">" | "<>" | ">"= | "<"=

<Операнд>

<Определение>

::= <Определение переменной> | <Условное определение>

<Определение локальной функции>

::= <Имя локальной функция> "("<Аргумент локальной функции>")" = <Выражение>

Примечание: <Выражение> в <Определении локальной функции> не может содержать: <Переменную> и спец. функции SUM и PROD

<Определение переменной>

::= <Дополнительная переменная> = <Выражение> <Разделитель>

<Перечисление аргументов>

::= <Переменная1>, ..., <Переменная2>

Примечание: <Переменная1> и <Переменная2> - должны иметь одинаковое имя и обязательно должны быть с числовым индексом! Причем индекс <Переменной1> должен быть меньше индекса <Переменной2>

<Переменная>

::= <Входная переменная> | <Дополнительная переменная>

<Переменная цикла>

::= i

Примечание: <Переменную цикла> можно использовать только внутри спец. функций SUM и PROD

Примеры формул

1. Z1 = sin(X1) Z2 = cos(X2) F= Z1^2 + Z2^2 2. Z1 = 3 // Уровень помехи Z2 = |X1| // Модуль X1 Z3 = abs(X2) // Это тоже модуль X2 F = Z2 - Z3 + Z1R(-1, 1) 3. // пример использования "умножения" по умолчанию Alfa=3X1 Beta=4Sin(2Pi*X1X2) F = Alfa + Beta 4. // пример использования локальных функций Y1(U) = |U| Y2(U) = (U-3)^2 - 1 Y3(U) = |U-5| F=min(Y1(X1), Y2(X1), Y3(X1))+ min(Y1(X2), Y2(X2), Y3(X2)) 5. // пример использования суммы и произведения Z1= sum(1, dim-1, Xi+1-Xi) // явно указываем пределы суммирования Z2= sum(Xi^i)+prod(cos(Xi)) // пределы суммирования по умолчанию i=1,dim F= Z1+Z2 6. // пример использования условного определения if (|X1| <= 1) then I0=1 else I0=0 F= X1^2 + I0*R(-1,1)

Программная реализация трансляции формулы

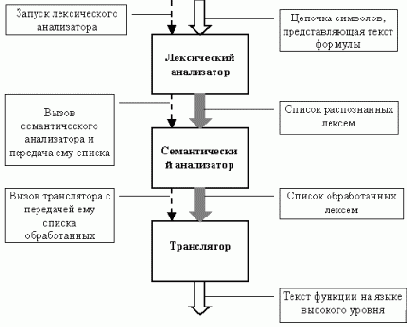
Обработка формулы состоит из следующих этапов:

Лексический анализ: входящий поток символов разбивается на лексемы. Выделение очередной лексемы производится путем посимвольного анализа теста формулы, разбор идет до тех пор, пока есть символы на входе. Если обнаружена неизвестная лексема, то разбор прекращается и выводится сообщение об ошибке с указанием места в тексте формулы, где была найдена эта лексема. После успешного завершения этого этапа будет сформирован список из "допустимых" лексем. Этот список можно использовать в побочных практических целях, например, выполнить "красивое" форматирование текста формулы.

Семантический анализ: список лексем проверяется, на то, что они образуют в совокупности допустимую формулу. Если обнаруживается ошибка, то выдается сообщение об ошибке с указанием места ошибки и ее описанием. Семантический анализатор построен по принципу конечного рекурсивного автомата, который каждая следующая лексема переводит из одного допустимого состояния в другое или выбрасывает исключительную ситуацию (переводит автомат в недопустимое состояние). Для каждого типа лексем есть набор правил (из выше описанной грамматики) определяющих как их анализировать в зависимости от текущего состояния автомата. После этого этапа получается список "обработанных" лексем. Этот список может отличаться от списка после первого этапа, так как семантический анализатор может добавлять, удалять и изменять лексемы в процессе анализа, например, будут добавлены лексемы умножения, которые согласно определению языка описания формул могут опускаться при записи формул.

Трансляция: опираясь на проверенный список лексем, формируется текст функции на языке высокого уровня которая, будучи скомпилированной, в составе некоторой программы будет вычислять заданную формулу.

Описанный подход можно представить в виде следующей схемы:

<Разделитель>

::= ; | <Перевод строки> | <Конец файла>

<Результирующие определение>

::= <Результат> = <Выражение> <Разделитель выражений>

Примечание: Весь текст формулы после <Результирующего определения> при анализе игнорируется

Структура формулы

Формула может состоять из следующих элементов: Определение локальной функции; Определение дополнительной переменной; Условное определение; Результирующее определение.

Первые три элемента могут присутствовать в произвольном количестве и порядке, однако переменные и локальные функции необходимо явно определять до их использования. Четвертый элемент всегда присутствует в формуле и находится в ее конце, весь дальнейший текст формулы после него игнорируется.

Типы данных

Предполагается, что все элементы формулы являются действительными числами, кроме следующих случаев: <Переменная цикла> (см. далее в описании грамматики), начальный и конечный индексы цикла (в функциях SUM и PROD), а так же константа DIM (размерность вектора входящих переменных) являются целыми положительными числами.

<Условие>

::= <Выражение> <Операция сравнения> <Выражение> | <Условие> (AND|OR) <Условие> | "(" <Условие> ")"

<Условное определение>

::= IF <Условие> THEN <Блок определений> | <Определение> [ELSE <Блок определений> | <Определение>]

<Вещественное число>

::= (<Целое число>.<Целое число>) | (<Целое число>[.<Целое число>]E[-|+]<Целое число>) | .<Целое число>[E[-|+]<Целое число>]

<Входная переменная>

::= X(<Целое число> | _i | _"("i ± <Целое число>")")

Примечание: <Входную переменную> у которой в индексе присутствует "i" можно использовать только внутри спец. Функций SUM и PROD

кто занимаются различными научными расчетами

Те, кто занимаются различными научными расчетами или написанием научного программного обеспечения часто сталкиваются со следующей проблемой: "Каким образом добавить возможность интерактивно вводить и вычислять математические формулы в своей программе?". Традиционно существует два подхода: "зашить" расчеты в исходный код программы; разрешить пользователю вводить в некотором редакторе описание задачи в виде совокупности формул, с последующей их обработкой некоторым математическим ядром.
К достоинствам первого подхода можно отнести скорость выполнения и минимальные размеры исполняемого модуля (если конечно все оптимально и аккуратно запрограммировано), а также возможность реализовать сколь угодно сложные и неформализованные задачи. Но этот подход не очень гибкий, так как пользователь может настраивать только параметры задачи, а если необходимо что-либо добавить или изменить - требуется изменять исходный код программы (что чревато известными трудностями, например, любые изменения требуют тестирования и отладки программы). Второй подход можно разделить на три основных направления: Использование спец. мат. пакетов в качестве серверов для вычисления формул; Интерпретация; Компиляция.
Конечно, можно использовать такие пакеты как MathLab, MathCad и т.п. для проведения научных и инженерных вычислений, но эти пакеты достаточно дорого стоят и, на мой взгляд, несколько "громоздкие". Этот подход можно рекомендовать тем, кто уже владеет подобными пакетами и знает, как их использовать для своих нужд. Основное преимущество данного подхода заключается в том, что эти пакеты "умеют" очень много. К недостаткам же можно отнести то, что они не поставляются в исходных кодах и поэтому представляют собой "черный ящик" со всеми вытекающими из этого неудобствами.
Интерпретация формул - достаточно распространенный подход и существует множество его реализаций. Достоинства: простота реализации, подробное диагностирование ошибок во время вычисления. Основным недостатком является крайне низкая скорость вычислений (хотя мне известны реализации с использованием кэширования и представления формул с использованием древовидных структур которые этим недостатком практически не обладают).
Компиляция - анализ и трансляция формул непосредственно в машинный код или в программу на языке высокого уровня. Преобразование формул в машинный код сопряжено со значительными трудностями, так как требует от разработчика глубоких знаний в этой области и к тому же привязывает реализацию к определенной аппаратной платформе. Гораздо более гибким способом является трансляция формул в программу на языке высокого уровня, так как это, во-первых, значительно упрощает сам процесс трансляции и, во-вторых, позволяет использовать этот подход практически без ограничений для любых программно-аппаратных платформ. К достоинствам этого подхода можно отнести высокую скорость вычислений, а к недостаткам, несколько более сложную обработку формул по сравнению с интерпретацией. Далее в этой статье будет рассмотрен именно этот подход - анализ и трансляция формул в программу на язык высокого уровня (на момент написания статьи реализована поддержка Object Pascal).

<Выражение>

Примечание: Если между выражениями пропущена <Операция>, то по умолчанию полагаем, что это операция умножения

и трансляции математических формул вот

Следует отметить, что рассмотренный в данной статье подход к разбору и трансляции математических формул вот уже более трех лет эффективно используется для описания тестовых задач глобальной оптимизации, которые состоят не только из функции качества, но еще и из произвольного количества ограничений в пакете глобальной поисковой непараметрической оптимизации "kaOptima". В упомянутом пакете, после трансляции формулы в программу (в данной реализации на языке Object Pascal), производится ее компиляция в динамически подключаемую библиотеку (dll) с помощью компилятора командной строки. Описанный подход можно легко адаптировать под любые другие языки программирования (например, язык С), при этом фактически надо только переписать процедуру трансляции списка обработанных лексем в программу на требуемом языке программирования.