Как звучат CD (Домыслы и реальность)
В.ФЕДОРОВ, г.Липецк.
На рынке бытовой аудиоаппаратуры прочно утвердился цифровой формат записи звуковых компакт-дисков (КД) Audio CD. В популярной любительской и профессиональной литературе различные авторы неоднократно высказывались по поводу достоинств и недостатков данного формата. В предлагаемой статье, опираясь на свой опыт, попытаюсь рассеять некоторые заблуждения.
В [1] автор указывает на нецелесообразность копирования компакт-кассет с компакт-дисков, ссылаясь при этом на то, что качество звучания КД, по его мнению, можно приравнять к качеству звучания аналоговой звуковоспроизводящей аппаратуры 3-го класса. В этой статье (что весьма интересно) автор поставил под сомнение теорему Шеннона (или, как ее называют в отечественной литературе, теорему Котельникова).
Предположим, что на вход аналого-цифрового преобразователя (АЦП) поступает сигнал с равномерно распределенным спектром в полосе частот от 0 до 20 кГц (рис.1 а). Если осуществлять аналого-цифровое преобразование с частотой дискретизации fg=44,1 кГц (несколько выше, чем по теореме Шеннона), а затем производить обратное цифро-аналоговое преобразование на той же fg, то в спектре аналогового сигнала, претерпевшего указанные преобразования, появятся паразитные полосы с центральными частотами, кратными fg (рис.1б). Упрощенно данное явление можно назвать трансформацией элементарных синусоидальных сигналов в сигналы сложной формы (например, описанный в [1] случай преобразования одиночного синусоидального сигнала 20 кГц в меандр с той же частотой).
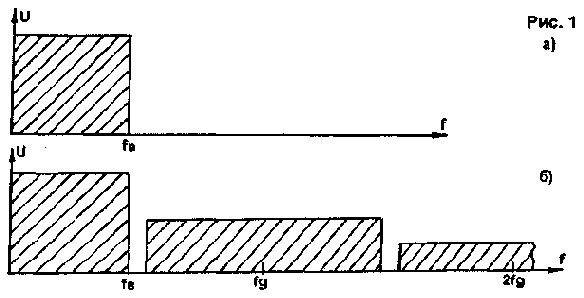
Puc.1
Для дальнейшего понимания сути происходящего обратимся к преобразованию гармонических периодических сигналов из временной области в частотную. На рис.2 графически отображен данный процесс. Во временной плоскости UOt построен график периодического сигнала. Если разложить функцию, изображенную на графике, используя дискретное преобразование Фурье (ДПФ), быстрое преобразование Хартли (БПХ) или современное дискретное косинусное преобразование (ДКП) на гармоники, и графически отобразить их амплитуду со сдвигом по частотной оси Of, то можно увидеть, что исходный сигнал в своем спектре содержит две гармоники с амплитудами U1 и U2. На практике временную зависимость амплитуды наблюдают с помощью осциллографов, а частотную - с помощью анализаторов спектра.
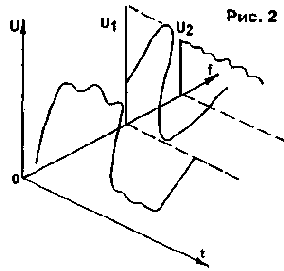
Puc.2
Если осуществить ДКП синусоидального и прямоугольного сигналов с частотой 20 кГц при fg=40 кГц, получится результат, изображенный на рис.3 а и б соответственно. Как можно видеть, в спектре прямоугольного сигнала, помимо основной частоты, имеется множество гармоник с частотами, кратными основной, и амплитудами, убывающими с ростом номера гармоники. Используя ФНЧ (т.е. вырезая все "лишние" гармоники), можно из прямоугольного получить синусоидальный сигнал. Обеспечить данный процесс можно как аналоговыми, так и цифровыми методами.

Puc.3
Если теперь, зная, что на выходе ЦАП сигнал из синусоидального становится прямоугольным, т.е. в спектре появляются паразитные полосы (рис.16), использовать ФНЧ с частотой среза fcp=20 кГц, из результирующего сигнала можно удалить все паразитные полосы, кратные fg. Активные ФНЧ п-го порядка обычно имеются во всех проигрывателях компакт-дисков (ПКД), если не прямо в схеме, то в составе интегральных ЦАП.
Паразитные гармоники в сигнале появляются из-за неидеальности АЧХ ФНЧ, включенных на входе и выходе АЦП и ЦАП (рис.4). В результате возникают наложения спектров формируемых ЦАПом сигналов, причем уровень паразитных составляющих тем меньше, чем "круче" АЧХ ФНЧ и больше затухание в его полосе заграждения.
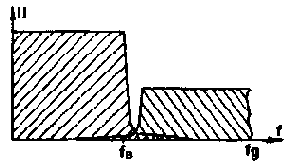
Puc.4
Увеличение fg в 4 или 8 раз относительно частоты Найквиста (верхней частоты сигнала) позволяет несколько раздвинуть составляющие спектра сигнала на выходе ЦАП, однако при этом неоправданно возрастает поток цифровых данных, сократить который средствами стандарта AudioCD нельзя.
Лишь улучшая характеристики ФНЧ до АЦП и после ЦАП, можно бороться с повышением помех, создаваемых боковыми паразитными полосами. Современные ПКД с ФНЧ не ниже 6 порядка относительно успешно справляются с задачей фильтрации сигнала после ЦАП, обеспечивая ослабление паразитных помех не менее 90 дБ. Полоса пропускания каналов звука при этом составляет 20...21600 Гц при неравномерности 5*10-3 дБ. Данные параметры заметно превосходят аналогичные параметры аналоговой звуковоспроизводящей аппаратуры всех классов.
Из вышеописанного можно сделать вывод, что при дискретизации сигнала с fg=2fB необходимо ужесточить требования к ФНЧ на выходе ЦАП ПКД.
В [1] автор также сообщает о компрессии сигнала перед записью на КД, а также об образовании завала частот в записях, произведенных с этих КД, в области 20...200 Гц. Точнее сказать, завал доходит до частоты 1 кГц, считающейся эталонной для техники звуковых частот.
Как следует из теории помехоустойчивости, при передаче сигналов (в т.ч. и звуковых), сигналы, имеющие большие динамический диапазон и полосу частот, перед передачей целесообразно компрессировать, что успешно ввел в обиход на практике американский исследователь Долби. Экспандирование сигнала осуществляется в ПКД по желанию пользователя. Стоит заметить, что в большинстве CD-ROM-драйвов, проигрывающих КД, экспандер фактически отсутствует. Его функцию заменяет ФНЧ, имеющийся в подавляющем большинстве звуковых карт и в активных колонках (кнопка "Bass"), который поднимает уровень басов, но никак не может являться полным аналогом экспандера.
Цифровая часть ПКД имеет возможность как корректировать, так и маскировать ошибки, причем могут исправляться как ошибки, обусловленные плохим качеством самой записи на КД, так и дефектами его поверхности. Однако нельзя переоценивать данную функцию ПКД, поскольку коды, используемые в нем для проверки, исправляют конечное число ошибок, а их количество при эксплуатации КД (механические повреждения), к сожалению, растет. Таким образом, при воспроизведении некачественных КД, особенно прошедших интенсивную эксплуатацию, качество звучания ПКД резко снижается.
В качестве примера приведу такой факт. Трехбитный корректирующий код четырехбитного слова (при коррекции Хэмминга) исправляет не более 1 ошибки. Следовательно, необходимо иметь такую запись, чтобы ошибка встречалась не чаще чем 1 раз на 7 бит информации. Конечно, в ПКД используются более мощные корректирующие коды, однако все равно имеется некоторый предел количества ошибок. Важную роль играют также качество аппаратуры, на которой производится запись КД; качество матрицы, с которой производится тиражирование КД при их массовом производстве; а также условия эксплуатации КД.
Существует мнение, что одно и то же музыкальное произведение, записанное на КД на разной аппаратуре, звучит по-разному. Это действительно так, ввиду того что ПКД пытается исправить (замаскировать) ошибки, возникающие при воспроизведении КД, записанных с помощью некачественной техники.
Схемотехнически процесс возникновения и маскировки ошибок изображен на рис.5. Пусть в моменты t1-t2 и t3-t4 на сигнал воздействует импульсная помеха (рис.5а). Корректирующее устройство отслеживает ее и замещает соседними "непораженными" отсчетами (рис.56), т.е. интерполирует сигнал. Однако если применить ДКП к полученному сигналу и проанализировать его спектр, в нем можно увидеть паразитные полосы. Если с ВЧ-составляющими успешно "борется" ФНЧ на выходе ЦАП, то более низкочастотные помехи накладываются на результирующий сигнал, создавая специфические искажения, особенно заметные при длительных помехах.
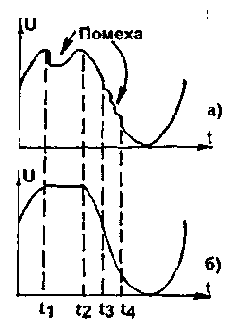
Puc.5
В литературе встречается указание на то, что так называемые "однобитные ЦАП" имеют худшие параметры, чем многобитные. В частности, большее значение фазового дрожания ("джиттера") наблюдается именно у однобитных ЦАП.
На рис.6 изображена функциональная схема однобитного ЦАП CS4328 фирмы Crystal Sem. Последовательные данные (могут быть представлены в 4-х форматах) поступают во входной преобразователь (ВП), преобразующий их в 18-разрядные параллельные потоки двух каналов. Сигналы через цифровые интерполя-торы (ЦИ) поступают на цифровые дельта-модуляторы (ДМ), которые формируют одноразрядные потоки данных с 64-кратной "сверхдискретизацией". Далее сигналы поступают на однобитные ЦАП, ФНЧ шестого порядка, и через буферные усилители подаются на выход схемы.
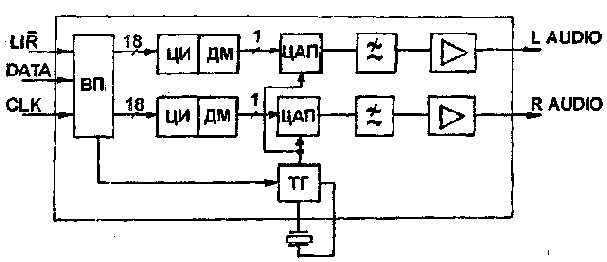
Puc.6
Поскольку в микросхеме используются более простые и дешевые однобитные ЦАП, стоимость прибора уменьшается при незначительном ухудшении его параметров. Тактовый генератор (ТГ), управляющий ЦАП, синхронизируется с помощью петли ФАПЧ приходящими синхроимпульсами CLK, что снижает уровень джиттера. Фильтр на переключаемых конденсаторах позволяет использовать схему на любых тактовых частотах (т.е. отсутствует необходимость перенастройки ФНЧ). Динамический диапазон микросхемы достигает 93 дБ.
Несомненно, на момент выпуска первых ПКД, устройства данного класса имели характеристики, сопоставимые или превышающие соответствующие характеристики аналоговой звуковоспроизводящей аппаратуры высшего класса. Схемные решения различных фирм-изготовителей отличались разнообразием, что вызвало продвижение на рынок моделей как высокого, так и низкого качества.
Приход на смену CD многопрофильного DVD-диска (звуковой версии) позволяет решить задачу фильтрации паразитных гармоник в спектре выходного сигнала цифровыми методами, а также путем увеличения частоты дискретизации. Поскольку в DVD-технологии используется MPEG-2 Audio-уплотнение данных, т.е. частотно-амплитудное представление сигнала посредством ДКП с последующим сокращением избыточности, появляется возможность эффективной цифровой фильтрации с использованием цифровых сигнальных процессоров.
Емкость однослойного DVD равна 4,7 Гб против 680 Мб КД, что позволяет записывать на DVD большие объемы данных. Однако поскольку в схемных решениях будут использоваться те же электронные приборы (АЦП, ЦАП и пр.), то так же остро будут стоять проблемы с уменьшением джиттера и т.п. Решать их будут фирмы, выпускающие электронные компоненты, путем проектирования более современных и качественных приборов.
На данный же момент ПКД является наиболее полноценной заменой морально устаревшей аналоговой аппаратуры воспроизведения звука.
Литература
1. Скулкин И. О качестве звука на компакт-дисках. - Радиолюбитель, 1998, N1.C.19
2. Золотухин И. и др. Цифровые звуковые магнитофоны. - Т. Радио и связь, 1990.
РЛ 8/2000, c.5-7.
