Задачи и практические вопросы к курсу
1. По каналу связи с нормальным белым шумом передается информация со скоростью Vпи
= 10 кбит/с. При этом средняя вероятность ошибок в канале составляет Pош = 10 -6.
Для улучшения качества передачи информации рассматривается несколько вариантов решения:
- кодирование корректирующим кодом с порождающей матрицей
G =
| 111 |;
- кодирование сверточным (6,3)-кодом;
- кодирование (8,4)-кодом Хемминга;
- уменьшение на 20% скорости передачи .
Какое из предложенных решений обеспечит больший эффект, если в первых трех случаях скорость передачи информации должна сохраниться прежней?
2. Порождающая матрица линейного блочного кода имеет вид
| G = | 1 0 1 0 1 0 | . | |||
| 0 1 0 1 0 1 |
Определить для данного кода H, dmin. Изобразить схему кодера и декодера.
Определить число ошибок, не исправленных данным кодом за 1 час работы, если Vпи
= 10 кбит/с, Рош = 10 -4.
3. В канале связи с шумами производится кодирование информации с использованием кода с порождающей матрицей вида G = | 11111 |.
На входе приемного устройства на интервале времени, соответствующем длине кодовой последовательности, присутствует колебание вида U(t) (рис. 4.1)
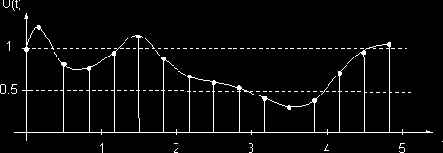

Рис. 4.1
Сигнал U(t)
в приемном устройстве подвергается дискретизации (по 3 отсчета на интервал, соответствующий одному символу кодовой последовательности).
Какое решение относительно m примет:
- жесткий мажоритарный декодер;
- мягкий декодер максимального правдоподобия?
4. Для кодера сверточного кода со схемой, показанной на рис. 2.5, определить k0, n0, m, n , k , R , b, изобразить кодовое дерево и решетчатую диаграмму, закодировать последовательность m = (1100100000..... , декодировать r с ошибкой во втором кадре с использованием алгоритма Витерби.
5. Предложить вариант схем кодера и декодера сверточного (9.6)-кода Вайнера-Эша (по аналогии с (12,9)-кодом), исправляющего одиночную ошибку на сегменте из трех кодовых кадров.
Проиллюстрировать работу кодера и декодера на примере.
6. Схема кодера линейного блочного кода приведена на рис. 4.2. Найти для него H, G, dmin, Pно , Рни. Изобразить схему синдромного декодера.
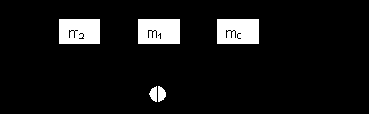

Рис. 4.2
7. Для сверточного кода со схемой рис. 2.5 ((6,3)-код) определить dmin , закодировать последовательность m = (1100000000...... , декодировать принятую последовательность с двойной ошибкой в третьем кадре с использованием алгоритма Витерби и Фано.
8. Изобразить схему кодера и декодера Меггитта для циклического (8,4)-кода. Привести пример кодирования и декодирования с одиночной ошибкой.
9. По каналу связи с шумами передается двоичная информация со скоростью Vпи
= 1 Мбит/с. При этом в среднем 1 раз в минуту в канале возникает ошибка.
Для уменьшения частоты ошибок предложено использовать несколько вариантов кодирования:
- (7,4)-кодом Хемминга;
- сверточным (6,3)-кодом;
- кодом с порождающей матрицей вида G = | 111 |.
Какое из предложенных решений обеспечит больший эффект, если скорость передачи информации Vпи должна остаться неизменной?
10. Предложить варианты схем кодера и декодера сверточного (15,12)-кода (по аналогии с (12,9)-кодом Вайнера-Эша, исправляющего одиночную ошибку на сегменте из трех кодовых кадров).
Привести пример кодирования и декодирования.
11. В цифровой двоичной системе связи информация передается со скоростью 2 Мбит/с, при этом в среднем один раз в минуту в канале возникает ошибка.
Как изменится частота появления ошибок, если в канале производить кодирование сверточным (6,3)-кодом и для сохранения скорости передачи информации в 2 раза повысить скорость передачи двоичных символов?
12. Изобразить схему декодера Меггитта для циклического (7,3)-кода. Привести пример кодирования и декодирования с одиночной ошибкой.
13. Порождающая матрица блочного кода имеет вид G = | 111 |. Найти H, dmin, Pно, Pни данного кода. Изобразить схему кодера и декодера.
14.
В канале связи с шумами производится кодирование информации с использованием блочного кода с порождающей матрицей G = | 11111 |. На входе приемного устройства присутствует колебание U(t) вида, показанного на рис. 4.3. Сигнал U(t) подвергается дискретизации, причем на интервал длительностью в один символ приходится два отсчета U(t).
Какое решение относительно m вынесет по принятой реализации:
- мягкий декодер максимального правдоподобия;
- жесткий мажоритарный декодер?
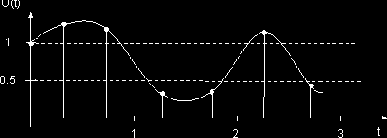

Рис. 4.3
15. Двоичный циклический код, заданный порождающим полиномом
g(x) = 1 + X2 + X3 + X4,
позволяет исправлять пакеты ошибок длиной 2 (двойные ошибки в соседних символах).
Определить длину кода. Сконструировать декодер Меггитта для данного кода.
16. Порождающая матрица линейного блочного кода G имеет вид
|
|
1 |
1 |
0 |
0 |
|
|
G = |
1 |
0 |
1 |
0 |
. |
|
|
1 |
0 |
0 |
1 |
|
Изобразить схему кодирования и декодирования с использованием данного кода. Определить время до первой не обнаруживаемой кодом ошибки, если скорость передачи составляет Vпи
= 1 Мбит/с, а вероятность ошибки в канале равна Pош
= 10 -7.
17. Изобразить схему, построить кодовое дерево и решетчатую диаграмму для несистематического сверточного кода с R = 1/3, m =
2 и имеющего порождающие полиномы вида
g1(x) = 1 + X + X2, g2(x) = 1 + X + X2 и g3(x) = 1 + X2.
18. По двоичному каналу связи передается информация со скоростью 9600 бит/с.
Сколько времени понадобится для передачи 1000 с. русского текста (энтропия H (l) = 2 бит/букву) с использованием примитивного равномерного двоичного кода и кода без избыточности ( одна страница - 2000 букв )?
19. Итеративный код задан матрицей вида


U = m2 m3 p1 .
p2 p3 p4
Записать порождающую матрицу эквивалентного ему линейного блочного систематического (n,k)-кода. Определить исправляющую способность кода, найти вероятность неисправления ошибки, если вероятность ошибок в канале составляет Pош = 10 -4 .
20. Итеративный код задан матрицей вида


U = m3 m4 m5 m3 + m4 m4 + m5
m6 m7 m8 m6 +m7 m7 + m8 .
m0+m3 m1+m4 m2+m5 p1 p2
m5+m6 m4+m7 m5+m8 p3 p4
Проверочные символы P1….P4 формируются путем суммирования всех информационных символов, входящих в соответствующие столбцы и строки матрицы, например p1 = m0 + m1 + m3 + m4 + m6 + m7 + m0 + m3 + +m1 + m4 + m2 + m5.
Записать порождающую матрицу эквивалентного линейного блочного систематического (n,k)-кода. Определить исправляющую способность кода. Найти вероятность не исправляемой данным кодом ошибки, если вероятность ошибки в канале составляет Pош = 10 -3.
21. Исправляющий двойные ошибки циклический (15,7)-код БЧХ имеет порождающий полином вида
G(x) = X8 + X7 + X6 + X4 + 1.
Построить кодер и декодер Меггитта для этого кода.
22. Дискретный источник выдает символы из ансамбля { ai } объемом К = 50.
Какое минимальное число разрядов должен иметь равномерный двоичный код, предназначенный для кодирования символов данного ансамбля? Записать примеры кодовых слов. Какова избыточность примитивного кода, если энтропия источника составляет 3 бит/букву?
23. Ансамбль дискретных символов { ai } объемом К = 32 имеет энтропию Н(А) = 2 бит/символ.
Найти минимальное количество кодовых символов, которое надо израсходовать на кодирование символа источника равномерным примитивным двоичным кодом.
Какое избыточное количество символов по сравнению с оптимальным кодом приходится использовать на один символ источника при примитивном кодировании?
24. Закодировать двоичным кодом Шеннона-Фано ансамбль { ai } , eсли вероятность символов имеет значения, приведенные ниже.
a1 a2 a3 a4 a5 a6 a7 a8
0.25 0.25 0.125 0.125 0.0625 0.0625 0.0625 0.0625
Найти среднее число символов кодовой комбинации. Определить избыточность кода.
25. В цифровой системе телевидения высокой четкости (ТВЧ) передача одного кадра изображения размером 1500*1000 элементов с числом градаций яркости М = 256 производится за Тк = 40 мс.
Какую полосу частот будет занимать цифровой телевизионный сигнал при использовании примитивной КИМ? Как изменится эта величина, если степень корреляции соседних элементов изображения составляет 0.95 и производится кодирование с полным устранением избыточности?
26. Некоторый дискретный источник выдает независимые символы из ансамбля { ai
} (i = 1,2,...9) с вероятностями, определенными следующим образом:
a1 a2 a3 a4 a5 a6 a7 a8 a9
0.2 0.15 0.15 0.12 0.1 0.1 .08 0.06 0.04
Закодировать символы данного ансамбля кодом Хаффмена. Построить кодовое дерево и определить среднюю длину кодового слова.
27. Циклический (15,4)-код задан порождающим полиномом вида
g(x) = X11+ X8 + X5 + X3 + X2 + X + 1.
Построить кодер и декодер Меггитта для этого кода. Определить минимальное хеммингово расстояние и исправляющую способность кода. Найти вероятность неисправления ошибки, если вероятность ошибки в канале составляет Pош = 10 -5.
28. Показать, что хороший декодер линейного блочного кода должен производить нелинейные операции, для чего доказать:
а) что процедура вычисления синдрома линейна по отношению к вектору ошибок, т.е. если S = F(e), то F(e1 +e2 )= F(e1
)+F(e2 );
б) что линейный декодер - это такой декодер, у которого функция e = f(S),
связывающая синдром и оценку вектора ошибок, удовлетворяет условию f (S1 +S2 ) = f(S1 )+f(S2 );
в) что если мы хотим, чтобы декодер исправлял все одиночные ошибки, то функция e = f(S), связывающая синдром и оценку вектора ошибок, должна быть нелинейной.
Доказать, что линейный декодер может исправлять не более n-k из n возможных одиночных ошибок.
29. Полиномиальный (17,9)-код задан порождающим многочленом вида
g(x) = X8 + X5 + X4 + X3 + 1.
Определить минимальное расстояние Хемминга для данного кода. Сколько ошибок может исправить этот код? Построить кодер и декодер Меггитта для данного кода. Определить вероятность не исправляемой кодом ошибки, если вероятность ошибки в канале составляет Pош = 10 -3.
30. Кодом с проверкой на четность называется код, который образуется путем добавления к k-разрядной информационной последовательности одного символа так, чтобы число единиц в полученном коде было четно.
Построить кодер и декодер для (8,7)-кода с проверкой на четность. Определить вероятность необнаруживаемой ошибки, если вероятность ошибки приема символа составляет
Pош = 10-3 . Изобразить схемы кодера и декодера.
31. Исправляющий три ошибки (23,12)-код является циклическим с порождающим полиномом
G(x) = X11 + X10 + X6 + X5 + X4 + X2 + 1,
или G(x) = X11 + X9 + X7 + X6 + X5 + X + 1.
Найти проверочный многочлен h(x) для данного кода. Построить кодер на основе g(x). Построить декодер Меггитта для данного кода.
32. Рассмотреть линейный блочный код, кодовое слово которого формируется по правилу :
U = (x0, x1, x2, x3, x4, x0+x1+x2+x3+x4, x0+x2+x3+x4, x0+x1+x2+x4, x0+x1+x2+x3 ).
Найти проверочную матрицу кода и параметры n, k
.
33. Добавить к коду из предыдущей задачи общую проверку на четность и построить соответствующую проверочную матрицу.
Чему равно минимальное кодовое расстояние полученного кода?
34. Построить для кодов из предыдущих задач порождающие матрицы по проверочным.
35. Двоичный код, предназначенный для кодирования сообщений источника с алфавитом M = 8, содержит следующие кодовые слова:
U1=00000; U2=10011; U3=01010; U4=11001;
U5=00101; U6=10110; U7=01111; U8=11100.
Является ли данный код линейным и систематическим?
Определить возможности кода по обнаружению и исправлению ошибок.
Если код является линейным, построить порождающую и проверочную матрицы кода, схемы кодирования и декодирования.
36. Спроектировать блоки кодирования и декодирования данных для системы передачи информации.
Исходные данные:
- источник выдает информацию блоками по 4 бита;
- производительность источника = 0,4 Мбит/с;
- используется (7,3)-код Хемминга;
- затухание сигнала на трассе D
= 150 дБ;
- коэффициент усиления передающей и приемной антенн G = 32;
- чувствительность приемника радиолинии N0 = 10 -18 Вт/Гц;
- прием сообщения - посимвольный с использованием ортогональных сигналов.
Определить мощность передатчика системы связи, обеспечивающую вероятность безошибочного приема блока сообщения P = 0,999999.
37. Одним из способов улучшения корректирующих свойств кодов является добавление общей проверки на четность (если число единиц в кодовом слове нечетно, добавляется 1 , если четно - 0), что эквивалентно перекодированию кодовых слов следующим образом:
U1 = m*G1
, U2 = U1*G2 .
Записать выражение для перекодирующей матрицы G2, соответствующей исходному (7,3)-коду Хемминга.
Записать выражение для проверочной матрицы нового кода. Изобразить схемы кодирующего и декодирующего устройств.
Как изменится вероятность необнаружения ошибки P(E) в сравнении с исходным (7,3)-кодом, если вероятность ошибки в канале Pош
= 10 -5 ?
38. По каналу связи передается информация со скоростью V = 2 кбит/с. Используются двоичные сигналы типа 1 и – 1. Мощность сигнала на входе приемника составляет P = 10 -14 Вт. Спектральная плотность мощности помех, привeденная ко входу, N0 = 10-18
Вт/Гц. При передаче используется корректирующий (7,3)-код Хемминга.
Определить число необнаруживаемых и неисправленных ошибок, проходящих по каналу связи за один час работы.
39. Для кодирования информации в системе связи используется (7,3)- код Хемминга. Скорость передачи - 1 кбит/с. В канале связи действует нормальная "белая" помеха со спектральной плотностью N0 = 10 -18
Вт/Гц.
При какой мощности сигнала на входе приемника вероятность неисправленной ошибки составит Pни
= 10 -8 ?
40. Порождающая матрица кода имеет вид


G = 0 1 0 0 1 0 1 .
0 0 1 0 0 1 1
Найти проверочную матрицу кода; изобразить схемы кодирующего и декодирующего устройств; найти минимальное кодовое расстояние кода; определить возможности кода по обнаружению и исправлению ошибок.
Определить вероятность пропуска необнаруживаемой ошибки P(E), если P ош
= 10 -6 .
41. Порождающая матрица кода имеет вид


0 1 0 0 0 1 1 1 0 1
G = 0 0 1 0 0 1 1 0 1 0 .
0 0 0 1 0 1 1 1 1 0
0 0 0 0 1 1 0 1 0 1
Найти проверочную матрицу кода; изобразить схемы кодирующего и декодирующего устройств; найти d кода; определить возможности кода по обнаружению и исправлению ошибок.
42. Проверочная матрица имеет вид
 |
|||
 |
|||
1 1 1 1 1 0 0 0
1 0 1 1 0 1 0 0 .
Н = 1 1 0 1 0 0 1 0
1 1 1 0 0 0 0 1
Найти порождающую матрицу кода; изобразить схемы кодирующего и декодирующего устройств; найти dmin
кода; определить возможности кода по обнаружению и исправлению ошибок.
43. С борта космического аппарата (КА) “ Марс 2002” передается телевизионное изображение поверхности планеты. Размер кадра изображения - 512*512 элементов, каждый элемент квантуется на 128 уровней и кодируется с использованием сверточного (6,3)-кода. Мощность передатчика КА - 100 Вт, коэффициент усиления антенны - G = 50.
Передача двоичных символов кодовых последовательностей осуществляется с использованием противоположных сигналов. Прием сигнала производится на антенну площадью S = 100 м2, чувствительность приемника - N
=10 -22 Вт/Гц.
За какое время может быть принят один кадр изображения, если прием производится посимвольно и отношение сигнал/шум по мощности на выходе приемника должно составить не менее 500? ( Расстояние до КА R = 50 млн. км.)
Как изменится это время, если вместо помехоустойчивого кодирования использовать передачу элементов изображения ортогональными сигналами и осуществлять прием в целом?
44. В ходе радиолокационного зондирования Венеры, осуществляемого радиолокатором с синтезированной апертурой, производилась передача радиоизображения поверхности кадрами размером 2048*128 элементов, причем каждый элемент квантовался на 64 уровня. Передача осуществлялась с использованием двоичной цифровой радиолинии, использующей противоположные сигналы.
Параметры радиолинии связи:
- мощность передатчика P = 50 Вт;
- коэффициент усиления антенны передатчика G = 40;
- площадь приемной антенны S = 300 м2
;
- чувствительность приемного устройства (спектральная плотность шумов, приведенная ко входу) N0 = 10-20
Вт/Гц;
- максимальное расстояние R =10 8 км.
Требуемое отношение сигнал/шум по мощности на выходе приемника радиолинии передачи изображения ( Pс / Pш ) = 1000 .
Сколько времени понадобится на передачу одного кадра изображения при посимвольном приеме? Как изменится это время, если кодирование элементов изображения производится сверточным (6,3)-кодом, исправляющим двойные ошибки?
45. В цифровой двоичной системе связи информация передается со скоростью 1 Мбит/с, при этом в среднем один раз в минуту в канале происходит ошибка.
Как изменится частота ошибок, если в канале использовать кодирование (7,3)-кодом Хемминга и для сохранения скорости передачи информации длительность передаваемых символов будет уменьшена в (7/3) раза? Определить величину выигрыша (проигрыша) по частоте ошибок за счет кодирования при средней вероятности ошибок в канале без кодирования Pош = 10 -3 … 10 -6.
46. Линейный блочный код задан порождающей матрицей G вида
 |
 |
1 0 0 1 1 0
G = 0 1 0 0 1 1 .
0 0 1 1 0 1
Изобразить схему кодера и синдромного декодера для этого кода. Составить таблицу декодирования с исправлением одиночных ошибок для декодера максимального правдоподобия.
47. Составить структурные схемы кодера и синдромного декодера для циклического (7,4)-кода, заданного порождающим полиномом
g( x ) = 1 + x + x3 .
Описать процесс кодирования и декодирования с исправлением одиночных ошибок.
48. Двоичный циклический код, заданный порождающим полиномом
g ( x ) = 1 + x2 + x3 + x4 ,
позволяет исправлять пакеты ошибок длиной 2 (двойные ошибки в соседних символах).
Чему равна длина этого кода?
Найти минимальное кодовое расстояние данного кода.
Сконструировать систематический кодер для этого кода.
Сконструировать декодер, позволяющий исправлять пакеты по 2 ошибки.
49. Построить кодирующее и декодирующее по схеме Меггитта устройства для циклического (15,11)-кода Хемминга, имеющего порождающий многочлен вида
g(x) = 1 + x +x4.
Сколько ошибок в принятой последовательности может обнаружить и исправить данный код?
50. Спроектировать блоки кодирования и декодирования для системы передачи данных со следующими исходными условиями:
- источник выдает непрерывный поток двоичных символов;
- производительность источника V = 0,3 Мбит/с;
- используется сверточный (12,9)-код Вайнера-Эша;
- декодирование сверточного кода - синдромное;
- затухание сигнала на трассе D = 160 дБ;
- коэффициент усиления передающей и приемной антенн G = 32;
- чувствительность приемника N0 = 10 -21
Вт/Гц;
- прием сигнала посимвольный с использованием ортогональных (противоположных) сигналов;
Oпределить мощность передатчика системы связи, обеспечивающего вероятность безошибочного приема символа сообщения P = 10-10.
51. Напряжение полезного сигнала на входе приемника U = 1 мкВ; входное сопротивление приемника R = 50 Ом ; сигналы противоположные; спектральная плотность помех на входе приемника N0 = 10 -13
Вт/Гц.
При какой длительности интервала наблюдения вероятность ошибочного различения двух противоположных сигналов составит Poш=10-5? Как изменится величина Рош, если использовать не противоположные, а ортогональные сигналы?
52. Действующее значение напряжения на входе приемника S = 1 мкВ; ширина полосы пропускания приемного устройства F = 10 кГц; спектральная плотность помех, приведенная ко входу, N0 = 10-17
Вт/Гц; входное сопротивление приемника R = 100 Ом.
Определить отношение сигнал/шум по мощности на входе приемника.
Определить вероятность ошибки при различении двух ортогональных сигналов длительностью t = 50 мс.
Построить график Рош(t) для t = 1мс....1с
.
53. Напряженность поля полезного сигнала в точке приема составляет E = 1 мкВ/м, действующая высота антенны h = 2.5 м, входное сопротивление приемника R = 75 Ом. Полоса пропускания входных цепей приемника F = 50 кГц, спектральная плотность помех, приведенная ко входу, N 0 = 10-17 Вт/Гц.
Определить отношение сигнал/шум по мощности на входе приемника, а также отношение сигнал/шум по энергии на выходе, если время приема составляет T = 10 мс.
При какой длине интервала наблюдения сигнала вероятность правильного приема составит 0.9999?
54. Радиолиния связи системы охранной сигнализации предназначена для передачи сигналов 0 - 1 ( 0 - охрана объекта не нарушена , 1 - охрана нарушена); сигналы 0 - 1 – ортогональные; прием сигнала ведется в соответствии с оптимальным правилом различения двух известных сигналов на фоне нормального белого шума.
Радиолиния имеет следующие параметры:
- напряженность поля сигнала в точке приема - 0.5 мкВ/м ;
- действующая высота антенны приемника - 1 м;
- входное сопротивление приемника - 100 Ом;
- полоса пропускания приемника - 2 кГц;
- чувствительность приемника равна 1 мкВ при отношении сигнал/шум по мощности в полосе приема 0 дБ.
Каким должен быть интервал когерентной обработки сигнала (время интегрирования в корреляторе), чтобы ложные тревоги в системе возникали с вероятностью не более 10 -9
?
55. Оптимальный приемник-различитель двух известных сигналов производит прием сигналов (сигналы - противоположные) на фоне нормального шума с равномерной в полосе ?Fпр спектральной плотностью N0 = 10-12 Вт/Гц. Мощность сигнала на входе приемника Рпр = 10-10 Вт, интервал приема сигнала Т ( время интегрирования ) - 0.1
с.
Определить мощность шумов на входе приемника при полосе ?Fпр = =10 кГц.
Определить вероятность ошибки при различении сигналов. Как изменится мощность шума, если полосу пропускания приемника сузить до ?Fпр = 100 Гц? Как при этом изменится вероятность ошибки различения?
56. Непрерывное сообщение A(t) с шириной полосы 2Fm = 10кГц передается по каналу связи с использованием простейшей KИM и посимвольного приема. Mощность полезного сигнала на входе приемника Р =10 -13 Вт.
Спектральная плотность мешающих шумов, приведенная ко входу, N0
= 10 -18 Вт/Гц, сигнал - типа 0 - 1.
Определить оптимальное с точки зрения отношения сигнал/шум на выходе приемника число уровней квантования сигнала.
57. На геостационарной орбите (Н = 40000 км) установлен спутник непосредственного ТВ вещания, работающий в обычном ТВ стандарте:
- однополосная модуляция;
- F = 6 МГц;
- P = 1 кВт;
- G = 100 .
Спектральная плотность мешающих шумов, приведенная ко входу приемника, N0 = 10 -21
Вт/Гц.
Kакую площадь должна иметь антенна приемника TВ сигнала, чтобы отношение сигнал/шум в канале изображения было не хуже (Pс /Pш ) =50 дБ.
58. Зaдача 57 при условии: частотная модуляция mчм = 3.
59. Какую мощность должен иметь передатчик радиолинии связи (портативный радиотелефон) с амплитудной модуляцией, если:
- чувствительность приемника при отношении сигнал/шум по мощности в полосе приема ( Рс
/ Рш ) = +10 дБ - 10 мкВ;
- действующая высота антенны приемника - 0.5 м ;
- полоса пропускания приемника - 20 кГц ;
- глубина амплитудной модуляции mам - 0.3;
- затухание сигнала в канале связи - не более 90 дБ;
и требуется обеспечить отношение сигнал/шум (Рс / Рш )вых
на выходе приемника не менее + 30 дБ.
60. Над охраняемой территориeй на высоте Н = 300 км пролетает разведывательный спутник, собирающий информaцию с aвтоматических перeдающих станций. Передатчик станции работает на ненаправленную антeнну (G = 1) и передает информацию блоками по 6 бит за 1 мс. Приeм сигнала нa спутнике осуществляется в целом. Площадь приемной антенны S = 1 м2. Спектральная плотность помех, приведенная ко входу приемника, N0
= 10 -17 Bт/Гц.
Kакую мощность должен иметь передатчик, чтобы вероятность правильного приема блока составляла не менее Рпр = 0,99999999 ?
Как изменится величина требуемой мощности, если перейти на посимвольный прием блока?
Как изменится вероятность правильного приема блока, если мощность передатчика не изменится, но прием производится посимвольно ?
61. Какую мощность должен иметь передатчик, установленный на геостационарном спутнике (Н = 40000 км), работающий на антенну с усилением G = 10
и передающий информацию с полосой 2Fm = 25 кГц с использованием:
1) AM;
2) ЧM, mчм = 10;
3) ВИМ, t = 10 мкс; DF = 10 мГц,
чтобы отношение сигнал/шум на выходе приемника было не менее 50 дБ? Площадь приемной антенны S
= 10 м2, спектральная плотность шумов приемника N0
= 10-18 Вт/Гц.
62. В системе связи с ВИM передается сообщение l(t) с полосой 2Fm = = 10 кГц. Для передачи используются 3 вида сигналов:
1) простой импульс t = 1мкс; S0
= 1В;
2) ЛЧM-импульс с t = 10 мкс; S0
= 0,1В; DF = 10 MГц;
3) ЛЧM-импульс с t
= 45 мкс; S0 = 0,5В; DF = 1 МГц.
При использовании какого сигнала отношение сигнал/шум на выходе приемника будет наибольшим?
63. Во сколько paз можно уменьшить мощность передатчика дискретной системы связи при переходе с посимвольного приема на прием в целом с использованием ортогональных сигналов, если передается одно из 128 известных сообщений и необходимо обеспечить вероятность правильного приема сообщения Р = 0,999999
?
64. Полоса системы связи с ВИМ DF = 1 MГц. Спектральная мощность шумов приемника N0 = 10 -16 Вт/Гц. Мощность сигнала на входе приемника P = 10 -10 Вт. Полоса передаваемого сообщения - 2Fm = 20 кГц.
Oпределить максимально достижимое отношение сигнал/шум в системе. При каком значении параметра сигнала t оно будет обеспечено?
65. С космического аппарата, находящегося в районе Mарса (R = =50 млн. км) передается телевизионное изображение. Размер кадра - 1000 * *1000 элементов. Tочность квантования элемента изображения бA /A = =5*10-3. Oсуществляется передача с использованием простейшей KИM, прием - посимвольный, сигналы 0-1 - противоположные.
Параметры радиолинии:
- P = 100 Вт;
- G = 100;
- S = 250 м 2;
- N0 = 10 -21 Вт/Гц.
За какое время может быть передан кадр изображения, если допустима вероятность ошибки в одном элементе изображения Pош = 0.00001? Как изменится это время, если прием элемента изображения производится в целом и сигналы Sj
- ортогональные?
66. При работе двоичной ШСС, передающей информацию ортогональными сигналами со скоростью 1 кбит/с и занимающей полосу ?F = 1 МГц, в среднем один раз в минуту допускается ошибка, обусловленная действием на входе приемника нормального белого шума. В общем канале связи может работать большое число систем связи с ШШС при условии, что сигналы различных систем ортогональны. Полагаем, что сигналы мешающих ШСС занимают ту же полосу, что и полезный сигнал, и уровни всех мешающих сигналов одинаковы и равны полезному сигналу.
При каком числе мешающих сигналов частота ошибок возрастет до одной ошибки в секунду?
67. На входе приемника двоичной ШСС, использующей для передачи символов 0 и 1 противоположные сигналы и передающей информацию со скоростью 10 кбит/с, спектральная плотность помех Nп в 50 раз превышает спектральную плотность полезного сигнала Ns.
Какую полосу должен иметь ШПС, чтобы вероятность ошибок при приеме не превышала Pош = 0.001?
68. В двоичной ШСС, использующей для передачи символов 0 и 1 ортогональные сигналы, спектральная плотность помех на входе приемника Nп в 100 раз превышает спектральную плотность сигнала Ns . Вероятность ошибок при передаче составляет P = 10-3. Полоса частот, занимаемых системой, ?F = 10 МГц.
Какова максимальная скорость передачи информации (кбит/с) при заданной вероятности Pош ?
69. Объем информации, накапливаемой метеоспутником за один виток вокруг Земли, составляет 10000 Мбайт. Сброс информации производится при пролете над станциями сбора метеоданных, при этом интервал устойчивой радиовидимости составляет 8 минут.
Передача информации производится байтами (8-битовыми словами) с использованием орто- гональных сигналов. Прием слова производится в целом. Система связи имеет следующие параметры:
- коэффициент усиления бортовой передающей антенны G = 100;
- мощность передатчика P = 10 Вт;
- высота орбиты спутника R = 5000 км;
- чувствительность приемника станции наблюдения N0 = 10 -21Вт/Гц;
- затухание сигнала в тропосфере D = 6 дБ.
Какую площадь должна иметь антенна станции наблюдения, чтобы вероятность ошибок при приеме одного слова не превышала Р = 0.000001 ?
70. Радиотелефон сотовой системы связи с модуляцией ВИМ - ШПС имеет следующие параметры :
- длительность импульса ВИМ-ШПС - 10 мкс;
- ширина полосы импульса ВИМ-ШПС - 10 МГц;
- частота дискретизации сообщения Fдискр = 2Fmax = 10 кГц ;
- индекс модуляции m вим - 0.5 ;
- минимальное энергетическое отношение сигнал/белый шум
на входе приемника - 300.
Какое число радиотелефонов может одновременно работать в отведенной полосе частот (10 мГц), если необходимо обеспечить отношение сигнал/шум на выходе приемника ( Рс/Рш
)вим не менее 30 дБ? (Учесть , что при несовпадении импульсов ВИМ-ШПС по времени они не создают взаимных помех).
71. Для повышения отношения сигнал/шум на выходе системы с КИМ при посимвольном приеме иногда используется так называемая КИМ с усиленным старшим разрядом. В такой КИМ для уменьшения вероятности ошибки в старшем разряде кода, вносящей наибольший вклад в ошибку приема сообщения, производится дополнительное кодирование этого разряда, например, путем увеличения длительности символа, соответ-ствующего этому разряду, или путем его многократной передачи и мажоритарного (по большинству) приема.
В системе цифрового вещания используется простейшая 13-разрядная КИМ с посимвольным приемом. Отношение сигнал/шум на выходе приемника с КИМ (с учетом шумов квантования и ошибок приема символов) составляет 76 дБ.
Как изменится отношение сигнал/шум на выходе приемника КИМ, если старший разряд кода подвергается трехкратной передаче и решение о его значении выносится по правилу " два из трех "?
72. Предыдущая задача при условии, что импульс, соответствующий старшему разряду кода, удлиняется вдвое в сравнении с остальными разрядами, что обеспечивает меньшую вероятность ошибки при его приеме.
73. Задача 71 при условии, что дублируется и мажоритарно принимается не только старший ( N-й ), но и N-1-й разряд кода.
74. Как изменится отношение сигнал/шум на выходе системы с условиями задачи 71, если передача производится с использованием не 13, а 15-разрядных слов ? Прием, как и ранее, посимвольный.
75. Как изменится отношение сигнал/шум на выходе приемника КИМ, если от посимвольной передачи и приема перейти к передаче блоками по три символа (пятнадцатиразрядное слово передавать как пять блоков по три символа) с кодированием блоков ортогональными сигналами S1....S8?
Предложить метод объединения символов исходной кодовой последовательности в блоки, обеспечивающий наилучшее качество приема сообщения.
76. При разработке системы низовой радиотелефонной связи предложены два альтернативных варианта ее построения:
1. КИМ - система с кодово-импульсной модуляцией и посимвольным приемом. Передачу символов 0 и 1 предполагается производить с использованием противоположных сигналов.
2. ВИМ-ШПС - система с время-импульсной модуляцией, в качестве импульса ВИМ использующая широкополосный шумоподобный сигнал Sшпс(t) .
В обоих случаях система должна отвечать следующим требованиям :
- частота дискретизации передаваемого сообщения Fдискр = 10 кГц;
- минимальное энергетическое отношение сигнал/шум на входе приемника, приведенное к интервалу дискретизации,
m = Ps*Tдискр
/ N0 > = 50;
- отношение сигнал/ шум по мощности на выходе приемника в худшем случае должно быть не менее + 30 дБ.
Какой из вариантов системы, удовлетворяющих заданным требованиям, будет менее широкополосным ?
Какая из систем обеспечит лучшее отношение сигнал/шум на выходе приемника, если полоса частот, занимаемая системой, не должна превышать 100 кГц?
77. Для условий предыдущей задачи рассмотреть варианты исполь-зования амплитудной и дискретной частотной модуляции.
78. Как изменится степень предпочтения различных вариантов постро-ения системы (задачи 77,78), если энергетическое отношение сигнал/шум в канале увеличить до 200 ?
79. Предприятие коммерческой связи предоставляет услуги по передаче дискретных сообщений по международной линии связи.
Передача производится с использованием алфавита { Ai } размером в 128 букв, простейшей КИМ без избыточного кодирования с посимвольным приемом. Параметры линии связи таковы, что при скорости передачи V = 33 кбит/с
в среднем допускается одна ошибка в секунду.
Плата, взымаемая с заказчика за передачу одной страницы текста ( 2 тыс. букв), составляет 50 коп .
Штраф, выплачиваемый заказчику за одну допущенную ошибку на страницу текста, - 2 грн .
Какова максимальная
прибыль, которую может получить предприятие связи за 1 час непрерывной работы?
80. Как изменится величина максимальной прибыли, если в канале применить помехоустойчивое кодирование (11,7)-кодом Хемминга, исправляющим одиночные ошибки ?
Как изменится размер прибыли (задача 79), если размер используемого алфавита { Ai
} уменьшится до 32 букв ?
81. По каналу связи с помехами с использованием двоичной системы связи (0-1) передается текстовая информация. Размер словаря сообщения (количество букв в тексте) К = 32. Средняя энтропия передаваемых сообщений составляет 3 бита/букву.
При скорости передачи Vп
= 9.6 кбит/с вероятность ошибки в канале составляет Pош
= 10-4.
Сумма, взымаемая с заказчика за передачу 1 кбита информации, составляет 20 коп.
Штраф, выплачиваемый заказчику за одну допущенную ошибку, - 1 грн.
Выбрать и обосновать наилучший способ передачи информации и найти скорость передачи, обеспечивающие максимальную прибыль за 1 час работы системы:
а) примитивное двоичное кодирование, передача с использованием сигналов типа 0 - 1;
б) то же, сигналы - ортогональные;
в) то же, сигналы - типа -1 +1;
г) варианты “а” и “б”, но с применением экономного кодирования;
д) варианты “а” и “б” с применением корректирующего кодирования (7,4)-кодом Хемминга;
е) варианты “а” и “б” с применением сверточного (6,3)-кода;
ж) одновременное применение экономного и корректирующего кодирования сверточным (6,3)-кодом.
82. По каналу связи с помехами с применением двоичной системы связи передается текстовая информация. Словарь сообщения (количество букв в тексте) К = 128. Средняя энтропия передаваемых сообщений составляет 4 бита/букву.
При скорости передачи Vп
= 100 кбит/сек вероятность ошибки в канале составляет Pош
= 10 -5.
Сумма, взымаемая с заказчика за передачу 1 кбита информации, составляет 5 коп. Штраф, выплачиваемый заказчику за одну ошибку, - 1 грн.
Предложить способ передачи информации и найти скорость передачи, обеспечивающие максимальную прибыль за 1 час работы системы:
а) примитивное двоичное кодирование, передача с использованием сигналов типа 0 - 1;
б) то же, сигналы - ортогональные;
в) то же, сигналы - типа -1 +1;
г) варианты “а” и “б” но с применением экономного кодирования;
д) варианты “а” и “б” с использованием корректирующего кодирова-ния (7,4)-кодом Хемминга;
е) варианты “а” и “б” с применением сверточного (6,3)-кода;
ж) одновременное применение экономного и корректирующего кодирования сверточным (6,3)-кодом;
з) вариант “ж”, но код (7,4);
и) переход на восьмеричную передачу с применением ортогональных сигналов;
к) любая из предложенных комбинаций, обеспечивающая наибольший эффект.
83. По каналу связи с помехами с использованием двоичной системы связи передается текстовая информация. Размер словаря сообщения К= 256 символов. Средняя энтропия передаваемых сообщений составляет 5 бит/букву.
При скорости передачи
Vп = 100 кбит/с вероятность ошибки в канале составляет Pош = 10-5.
Какой из способов передачи даст лучший эффект в смысле числа ошибок:
- кодирование сверточным (6,3)-кодом;
- безызбыточное кодирование;
- и то и другое?
84. С борта орбитальной станции «АЛЬФА» с использованием цифровой системы передачи данных передается телевизионное изображение поверхности планеты. Размер кадра изображения NxM элементов. Изображение подвергается скалярному квантованию и сжатию с применением эффективного алгоритма Хаффмена. Поток двоичных данных кодируется с использованием (n,k)-сверточного кода.
Сколько времени понадобится для приема одного кадра изображения, если прием производится посимвольно, декодирование принятой последовательности - с использованием алгоритма Витерби и отношение сигнал/шум по мощности на выходе приемника должно составить не менее В дБ?
Как изменится это время, если отказаться от корректирующего кодирования и считать, что Рош
= Рнеиспр ?
При какой скорости передачи данных отношение сигнал/шум на выходе приемника ухудшится вдвое в сравнении с максимально достижимым?
Выполнить задание с использованием исходных данных, приведенных в табл. 4.1.
Таблица 4.1
|
Номер варианта / Исходные данные |
1 |
2 |
3 |
|
Размер кадра изображения элементов M x N |
512х512 |
512х1024 |
512х2048 |
|
Число уровней квантования |
256 |
512 |
256 |
|
Средняя энтропия источника H(Y) бит/пиксел |
2 |
3 |
2,5 |
|
Параметры сверточного кода (n,k) |
(6,3) |
(8,4) |
(4,2) |
|
Мощность передатчика P, Вт |
10 |
12 |
15 |
|
Коэффициент усиления передающей антенны G |
200 |
100 |
150 |
|
Несущая частота радиолинии F0 , ГГц |
11 |
12 |
14 |
|
Затухание сигнала в тропосфере D, дБ |
4 |
6 |
8 |
|
Высота орбиты H, км |
500 |
400 |
1000 |
|
Площадь приемной антенны S, м2 |
100 |
200 |
50 |
|
Чувствительность приемника N 0, Вт/Гц |
10-20 |
5х10-21 |
10-21 |
|
Отношение сигнал/шум по мощности на выходе приемника B, дБ |
40 |
50 |
44 |
85. При разработке системы высококачественной радиотелефонной связи предложены два альтернативных варианта ее построения:
- КИМ - система с кодово-импульсной модуляцией и посимвольным приемом; передачу символов 0 и 1 предполагается производить с использованием противоположных (КИМ-ФМ) или ортогональных (КИМ-ЧМ) сигналов;
- ВИМ - ШПС - система c время-импульсной модуляцией, в качестве импульса ВИМ использующая широкополосный сигнал S шпс(t) .
В обоих случаях система должна отвечать следующим требованиям:
- минимальное энергетическое отношение сигнал/шум на входе приемника, приведенное к интервалу дискретизации, m = Ps·Tдискр /N0
>m min;
- отношение сигнал/шум по мощности (с учетом шумов квантования при КИМ) на выходе приемника в худшем случае должно быть не менее Вmin дБ.
Изобразить функциональную схему приемника РТС
для обоих вариантов построения.
Обосновать выбор числа уровней квантования сигнала в системе с КИМ, обеспечивающего наибольшее отношение сигнал/шум на выходе приемника при заданном m .
Какой из вариантов системы, удовлетворяющих заданным требованиям, будет менее широкополосным?
Какая из систем обеспечит лучшее отношение сигнал/шум на выходе приемника, если полоса занимаемых частот не должна превышать DF ?
Как изменится степень предпочтения, если полосу частот, занимаемую системой, сократить вдвое?
Как изменится степень предпочтения различных вариантов построения системы, если отношение сигнал/шум в канале m увеличить вдвое?
Выполнить задание с использованием исходных данных табл. 4.2.
Таблица 4.2
|
Номер варианта / Исходные данные |
1 |
2 |
3 |
|
Частота дискретизации сигнала F дискр, кГц |
10 |
8 |
15 |
|
Энергетическое отношение сигнал/шум m |
50 |
100 |
150 |
|
Отношение сигнал/шум по мощности на выходе B , дБ |
50 |
60 |
55 |
|
Допустимая полоса частот DF , кГц |
100 |
100 |
150 |
|
Индекс время-импульсной модуляции m вим |
0.5 |
0.7 |
0.6 |
|
Способ передачи сигнала с КИМ |
КИМ-ЧМ |
КИМ-ФМ |
КИМ-ЧМ |
86. Изобразить функциональную схему, построить кодовое дерево и решетчатую диаграмму для линейного сверточного (n,k)-кода, заданного порождающими полиномами G1(X) и G2(X).
Закодировать последовательность вида m = ( 101101...., внести в принятую последовательность одиночную ошибку и с использованием алгоритма Витерби (Фано) декодировать принятую последовательность r.
Определить вероятность пропуска неисправляемой ошибки
Pнеиспр при вероятности ошибки в канале Pош.
Изобразить временные диаграммы работы схемы при подаче на ее вход кодируемой последовательности m вида ( 101101......
Выполнить задание с использованием данных табл. 4.3.
Таблица 4.3
|
Параметры кода n, k, r |
6,3,1/2 |
4,2,1/2 |
8 |
|
Коэффициенты порождающего полинома G1(X) |
111 |
10 |
1000 |
|
Коэффициенты порождающего полинома G2(X) |
101 |
11 |
1001 |
|
Принятая последовательность r |
11010001010010…. |
110101000100… |
10100010100010…. |
|
Вероятность ошибки в канале Pош |
10-5 |
10-6 |
10-4 |
87. По каналу связи с помехами с использованием двоичной системы связи передается текстовая информация.
Энергетические параметры канала связи таковы, что при скорости передачи Vп, кбит/с, вероятность ошибки в канале (обусловленной действием белого шума) составляет Pош.
Сумма, взымаемая с заказчика за безошибочную передачу 1 кбита информации, составляет 0.05 грн. Штраф, выплачиваемый заказчику за одну ошибку, допущенную при приеме переданного сообщения, - 1 грн.
Изменяя скорость передачи информации, способ передачи и приема, параметры используемых сигналов, обеспечить максимальную величину чистой прибыли, получаемой за 1 час непрерывной работы системы.
Мощность передатчика и чувствительность приемника считать неизменными.
Оптимизацию проводить в рамках следующих вариантов построения системы:
- используется примитивное двоичное кодирование, передача ортогональными сигналами;
- то же, сигналы противоположные;
- применяется экономное кодирование с полным устранением избыточности в сообщении;
- используется помехоустойчивое кодирование (7,4)-кодом Хемминга;
- применяется помехоустойчивое кодирование (6,3)-сверточным кодом.
- одновременно используются все рассмотренные меры, обеспе-чивающие повышение чистой прибыли от системы.
Как изменится величина прибыли, если размер алфавита источника увеличится вдвое?
Выполнить задание с использованием данных табл. 4.4.
Таблица 4.4
|
Номер варианта / Исходные данные |
1 |
2 |
3 |
|
Размер алфавита источника K |
128 |
256 |
128 |
|
Средняя энтропия передаваемого сообщения H, бит/букву |
3 |
4 |
3,5 |
|
Исходная скорость передачи Vп , кбит/c |
9,6 |
19,2 |
2,4 |
|
Вероятность ошибки в канале при заданной скорости Vп - Pош |
10-6 |
10-5 |
10-7 |
При решении задач можно пользоваться приведенной ниже таблицей значений интеграла вкроятности 1 - Ф(Z) – табл. 4.5.
Таблица 4.5
|
Z |
1 - Ф(Z) |
|
0 |
0.5 |
|
0.1 |
0.46 |
|
0.2 |
0.42 |
|
0.5 |
0.31 |
|
0.8 |
0.21 |
|
1.0 |
0.16 |
|
1.2 |
0.115 |
|
1.5 |
0.067 |
|
2.0 |
0.0227 |
|
2.2 |
0.0122 |
|
2.5 |
0.0062 |
|
3.0 |
0.0013 |
|
3.5 |
2*10(-4) |
|
4.0 |
3.16*10(-5) |
|
4.5 |
4.43*10(-6) |
|
5.0 |
2.86*10(-7) |
|
6.0 |
9.86*10(-10) |
|
7.0 |
1.28*10(-12) |
|
8.0 |
6.22*10(-16) |
|
9.0 |
1.13*10(-19) |
Библиографический список
1. Лезин Ю.С. Введение в теорию и технику радиотехнических систем. - М.: Радио и связь, 1986.
2. Зюко А.Г., Коробов Ю.Ф. Теория передачи сигналов. - М.: Сов. радио, 1972.
3. Радиотехнические системы/ Под ред. Ю.М. Казаринова - М.: Сов. радио, 1968.
4. Чердынцев В.А. Радиотехнические системы. – Минск: Вышэйш. шк., 1988.
6. Пенин П.И. Системы передачи цифровой информации. - М.: Сов. радио, 1976.
7. Мордухович Л.Г., Степанов А.Г. Системы радиосвязи (курсовое проектирование). - М.: Радио и связь, l987.
8. Гуткин Л.С. Проектирование радиосистем и радиоустройств. - М.: Радио и связь, 1986.
9. Пестряков В.Б., Кузенков В.Д. Радиотехнические системы. - М.: Радио и связь, 1988.
10. Калинин А.Н., Черенков Е.П. Распространение радиоволн и работа радиолиний. - М.: Радио и связь, 1971.
11. Справочник по радиорелейной связи/ Под peд. С.В. Бородича - М.: Радио и связь, 1981.
I2. Коржик В.И., Финк Л.М., Шелкунов К.Н.. Расчет помехоустойчивости систем передачи дискретных сообщений. - М.: Радио и связь, 1981.
13. Тепляков И.П., Рощин Б.В. Радиосистемы передачи информации. - М.: Радио и связь, 1982.
14. Банкет В.Л., Дорофеев В.П. Цифровые методы в спутниковой связи. - М.: Радио и связь, 1988.
15. Кларк Дж., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. – М.: Радио и связь, 1987.
16. Кузьмин И.В. Основы теории информации и кодирования. - Минск: Вышэйш. шк., 1986.
17. Хемминг Р.В. Теория информации и теория кодирования. - М.: Радио и связь, 1983.
Оглавление
1. Основы помехоустойчивого кодирования ………………………………….3
1.1. Основные принципы. Типы кодов. 3
1.2. Линейные блочные коды.. 5
1.2.1. Код с проверкой на четность. 6
1.2.2. Итеративный код. 9
1.2.3. Порождающая матрица линейного блочного кода. 10
1.2.4. Проверочная матрица. 14
1.2.5. Дуальные коды.. 15
1.2.6. Синдром и обнаружение ошибок. 16
1.2.7. Синдромное декодирование линейных блочных кодов. 18
1.2.8. Мажоритарное декодирование линейных блочных кодов. 21
1.2.9. Декодирование методом максимального правдоподобия. 23
1.2.10. Вес и расстояние Хемминга. Способность кодов обнаруживать и исправлять ошибки. 27
1.3. Полиномиальные коды.. 32
1.3.1. Циклические коды.. 34
1.3.2. Кодирование с использованием циклических кодов. 34
1.3.3. Вычисление синдрома и исправление ошибок в циклических кодах ………………………………………………………………………...39
1.3.4. Неалгебраические методы декодирования циклических кодов. 41
2. Сверточные коды.. 45
2.1. Кодирование с использованием сверточных кодов. 45
2.2. Синдромное декодирование сверточных кодов. 49
2.3. Кодовое дерево и решетчатая диаграмма. 51
2.4. Декодирование сверточных кодов. Алгоритм Витерби. 53
2.5. Алгоритмы поиска по решетке. 56
3. Применение корректирующего кодирования в системах связи. 58
3.1. Каскадные коды.. 58
3.2. Кодирование с перемежением. 59
4. Задачи и практические вопросы к курсу. 62
Библиографический список ………………………………………………85
