Вычисление синдрома и исправление ошибок в циклических кодах
Вычисление синдрома для циклических кодов является довольно простой процедурой.
Пусть U(x)
и r(х) ? полиномы, соответствующие переданному кодовому слову и принятой последовательности.
Разделив r(x)
на g(x), получим
r(x) = q(x)× g(x) + s(x), (1.73)
где - q(x) — частное от деления, s(x)
— остаток от деления.
Если r(x)
является кодовым полиномом, то он делится на g(x) без остатка, то есть s(x) = 0.
Следовательно, s(x) ¹ 0 является условием наличия ошибки в принятой последовательности, то есть синдромом принятой последовательности.
Синдром s(x)
имеет в общем случае вид
S(x) = S0 + S1 × x + ... + Sn- k-1 × xn-k-1 . (1.74)
Очевидно, что схема вычисления синдрома является схемой деления, подобной схемам кодирования рис. 1.10 или 1.11 .
При наличии в принятой последовательности r хотя бы одной ошибки вектор синдрома S будет иметь, по крайней мере, один нулевой элемент, при этом факт наличия ошибки легко обнаружить, объединив по ИЛИ выходы всех ячеек регистра синдрома.
Покажем, что синдромный многочлен S(x) однозначно связан с многочленом ошибки e(x), а значит, с его помощью можно не только обнаруживать, но и локализовать ошибку в принятой последовательности.
Пусть
e(x) = e0 + e1 × x + e2 × x2 + ... + en-1 × x n-1 (1.75)
— полином вектора ошибки.
Тогда полином принятой последовательности
r(x) = U(x) + e(x). (1.76)
Прибавим в этом выражении слева и справа U(x), а также учтем, что
r(x) = q(x)× g(x) + S(x), U(x) = m(x)× g(x), (1.77)
тогда

то есть синдромный полином S(x)
есть остаток от деления полинома ошибки e(x) на порождающий полином g(x).
Отсюда следует, что по синдрому S(x) можно однозначно определить вектор ошибки e(x), а следовательно, исправить эту ошибку.
На рис. 1.14 приведена схема синдромного декодера с исправлением однократной ошибки для циклического (7,4)-кода. По своей структуре она подобна схеме, приведенной на рис. 1.6, с той лишь разницей, что вычисление синдрома принятой последовательности производится здесь не умножением на проверочную матрицу, а делением на порождающий полином. При этом она сохраняет и недостаток, присущий всем синдромным декодерам: необходимость иметь запоминающее устройство, ставящее в соответствие множеству возможных синдромов S
множество векторов ошибок e. Цикличность структуры кода в этом случае не учитывается.
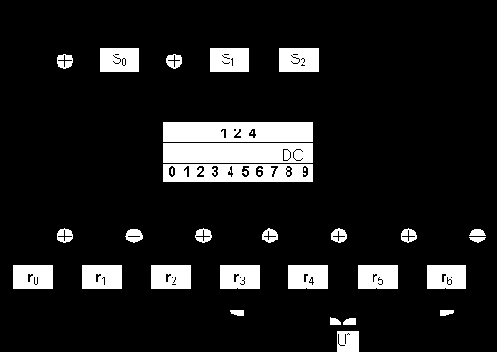
Рис. 1.14
