Порождающая матрица линейного блочного кода
Только что в качестве примера были рассмотрены два простейших корректирующих кода - код с простой проверкой на четность, позволяющий обнаруживать однократную ошибку в принятой последовательности, и блочный итеративный код, исправляющий одну ошибку с помощью набора проверок на четность по строкам и столбцам таблицы. Однако формальное правило, по которому осуществляется кодирование, то есть преобразование информационной последовательности в кодовое слово, по-настоящему еще не определено. Так как же задаются блочные коды?
Простейшим способом описания, или задания, корректирующих кодов является табличный способ, при котором каждой информационной последовательности просто назначается кодовое слово из таблицы кода (табл. 1.2)
Таблица 1.2
| m | U | ||
| 000 | 0000 | ||
| 001 | 0011 | ||
| 010 | 0101 | ||
| 011 | 0110 | ||
| 100 | 1001 | ||
| 101 | 1010 | ||
| 110 | 1100 | ||
| 111 | 1111 |
Такой способ описания кодов, кстати, применим для любых, а не только линейных кодов. Однако при больших k размер кодовой таблицы оказывается слишком большим, чтобы им пользоваться на практике (для кода с простой проверкой на четность двухбайтового слова размер таблицы составит ~ 25 * 216 = 2000000 двоичных символов).
Другим способом задания линейных блочных кодов является использование так называемой системы проверочных уравнений, определяющих правило, по которому символы информационной последовательности преобразуются в кодовые символы. Для того же примера система проверочных уравнений будет выглядеть следующим образом:
U0
= m0,
U1
= m1, (1.9)
U2
= m2,
U3
= m0 + m1 + m2.
Однако наиболее удобным и наглядным способом описания линейных блочных кодов является их задание с использованием порождающей матрицы, являющейся компактной формой представления системы проверочных уравнений:
|
|
1 0 0 … 0 |
P00 P01 . . . . P0, n- k- 1 |
|
|
G = |
0 1 0 … 0 |
P10 P11 . . . . P1, n- k- 1 |
|
|
|
……… |
……………… |
. (1.10) |
|
|
0 0 0 … 1 |
Pk- 1, 0 Pk- 1, 1 . . . . Pk- 1, n- k- 1 |
|
|
единичная матрица I k*k |
матрица Р k*(n- k) |
размером k *
n
с двоичными матричными элементами. При этом каждое кодовое слово является линейной комбинацией строк матрицы G, а каждая линейная комбинация строк G - кодовым словом.
Пусть m = (m0 , m1 ,. . . , mk -1) будет тем блоком-сообщением, который необходимо закодировать с использованием данного кода.
Тогда соответствующим ему кодовым словом U будет
U = m× G
. (1.11)
С учетом структуры матрицы G символы кодового слова U будут такими:
для i = 0, 1, 2,. . . , k- 1
Ui
= mi ; (1.12)
для i = k, k+1,. . . , n
Ui = m0× P0j + m1× P1j + m2× P2j +…+ mk- 1× Pk- 1, j . (1.13)
Иными словами, k крайних левых символов кодового слова совпадает с символами кодируемой информационной последовательности, а остальные (n - к) символов являются линейными комбинациями символов информационной последовательности.
Определенный таким образом код называется линейным блочным систематическим (n,k)-кодом с обобщенными проверками на четность, а задающая его матрица G называется порождающей матрицей кода.
В качестве примера рассмотрим известный (7,4)-код Хемминга, являющийся классической иллюстрацией простейших кодов с исправлением ошибок.
Пусть m = (m0, m1, m2, m3) будет тем сообщением, или информационной последовательностью, которую нужно закодировать.
Порождающая матрица G для (7. 4)-кода Хемминга имеет вид
|
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
|
G(7,4) = |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
. |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
(1.14) |
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
|
U = m× G = ( m0 m1 m2 m3 ) |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
= |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
= (m0 , m1 , m2 , m3 , m0 + m2 + m3 , m0 + m1 + m2 , m1 + m2 + m3 ), (1.15)
или
U0 = m0 ,
U1 = m1 ,
U2 = m2 ,
U3 = m3 , (1.16)
U4 = m0 + m2 + m3 ,
U5 = m0 + m1 + m2 ,
U6 = m1 + m2 + m3 .
Например, пусть m = ( 1 0 1 1
) , тогда соответствующее кодовое слово будет иметь вид U = ( 1 0 1 1 1 0 0 ). Или другой пример: пусть m = ( 1 0 0 0
), тогда U = ( 1 0 0 0 1 1 0 ).
Интересно отметить, что в соответствии с приведенным выше определением строки матрицы G сами являются кодовыми словами данного кода, а все остальные кодовые слова - линейными комбинациями строк порождающей матрицы.
На основании порождающей матрицы G(7,4) (1.15) или приведенной системы проверочных уравнений (1.16) легко реализовать схему кодирования для рассматриваемого (7,4)-кода Хемминга (рис. 1.4).
Кодер работает точно так же, как и при простой проверке на четность, но теперь выполняет не одну общую, а несколько частичных проверок, формируя, соответственно, несколько проверочных символов.
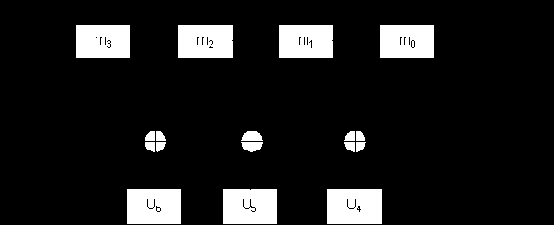
Рис. 1.4
