Неалгебраические методы декодирования циклических кодов
Все методы декодирования линейных блочных кодов можно разбить на две группы: алгебраические и неалгебраические.
В основе алгебраических методов лежит решение систем уравнений, задающих значение и расположение ошибок. Рассмотренные синдромные декодеры относятся именно к этой группе методов.
При неалгебраических методах та же цель достигается с помощью простых структурных понятий теории кодирования, позволяющих находить комбинации ошибок более простым путем.
Одним из неалгебраических методов является декодирование с использованием алгоритма Меггитта, пригодного для исправления как одиночных, так и l-кратных ошибок (на практике l £ 3).
При декодировании в соответствии с алгоритмом Меггитта также вычисляется синдром принятой последовательности S(x), однако используется он иначе, нежели в рассмотренных ранее синдромных декодерах.
Идея, лежащая в основе декодера Меггитта, очень проста и основывается на следующих свойствах циклических кодов:
- существует взаимно-однозначное соответствие между множеством всех исправляемых ошибок и множеством синдромов;
- если S(x) — синдромный многочлен, соответствующий многочлену ошибок е(x), то x×S(x) mod g(x) — синдромный многочлен, соответствующий x× e(x) mod (xn + 1).
Равенство а(x) = b(x) mod p(x) читается как “а(x), сравнимо с b(x) по модулю р(x)” и означает, что а(x) и b(x) имеют одинаковые остатки от деления на полином p(x).
Таким образом, второе условие означает, что если комбинация ошибок циклически сдвинута на одну позицию вправо, то для получения нового синдрома нужно сдвинуть содержимое регистра сдвига с обратными связями, содержащего S(x), также на одну позицию вправо.
Следовательно, основным элементом декодера Меггитта является сдвиговый регистр. Структурная схема декодера Меггитта для циклических кодов произвольной длины приведена на рис. 1.15.

Рис. 1.15
Декодер работает следующим образом. Перед началом работы содержимое всех разрядов регистров равно нулю. Принимаемая последовательность r в течение первых n
тактов вводится в буферный регистр и одновременно с этим в (n-k)-разрядном сдвиговом регистре с обратными связями производится ее деление на порождающий полином g(x).
Через n тактов в буферном регистре оказывается принятое слово r , a в регистре синдрома — остаток от деления вектора ошибки на порождающий полином.
Вычисленный синдром сравнивается со всеми табличными синдромами, и в случае совпадения с одним из них старший разряд буферного регистра исправляется путем прибавления к его значению единицы.
После этого синдромный и буферный регистры один раз циклически сдвигаются. Это реализует умножение S(x) на x и деление на g(x). Содержимое ячеек синдромного регистра теперь равно остатку от деления x×S(x) на g(x)
или синдрому ошибки x× е(x) mod (Хn + 1).
Если новый синдром совпадает с одним их табличных, то исправляется очередная ошибка и т.д. Через n тактов все позиции будут, таким образом, исправлены.
Рассмотрим работу декодера Меггитта для циклического (7,4)-кода, исправляющего одиночную ошибку. Схема декодера изображена на рис. 1.16.

Рис. 1.16
Принцип работы декодера заключается в том, что независимо от того, в какой позиции произошла ошибка, осуществляется ее сдвиг в последнюю ячейку буферного регистра с соответствующим пересчетом синдрома и ее исправление в этой позиции.
Полином ошибки в старшем разряде для (7,4)-кода Хемминга имеет вид е6 (x) = x6, соответствующий ему синдромный полином S6 (x) = 1 + x3 ( S = (101)), детектор ошибки настроен на это значение синдрома.
Пусть, например, передана последовательность U = (1001011), ей соответствует кодовый полином U(x) = 1 + x3 + x5 + x6. Произошла ошибка в третьей позиции е(x) = x3, принятый вектор имеет вид r = (1000011), его полином r(x) = 1 + x5 + x6.
Kогда принятая последовательность полностью входит в буферный регистр, в регистре синдрома оказывается синдром, соответствующий ошибке е(x) = x3 S3 = (110). Поскольку он не совпадает с табличным для е6, на выходе детектора ошибок будет 0 и исправления не происходит.
Далее производятся однократный циклический сдвиг принятой последовательности в буферном регистре, однократное деление синдрома x•S3 на порождающий полином в регистре с обратными связями и проверка на совпадение синдрома с заданным.
Последовательность состояний регистров декодера в процессе декодирования показана на рис. 1.17.
Рис. 1.17
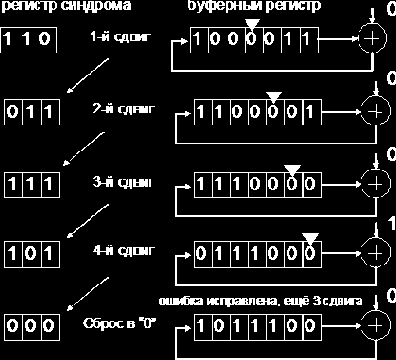
тактов производится ввод принятой последовательности в буферный регистр, в течение l тактов — исправление ошибки, и еще в течение n
- l - восстановление буферного регистра в исходное состояние с исправленным словом. Простота декодера достигается увеличением времени декодирования.
Следует отметить, что в связи с успехами в разработке БИС и устройств памяти в значительной степени снимается вопрос о размерах таблиц, связывающих значения синдрома и вектора ошибки (для синдромных декодеров) и даже значения кодовых слов и принятых последовательностей (для декодера максимального правдоподобия). Поэтому в перспективе возможно снижение интереса к кодам, обладающим специальной структурой, и к методам их декодирования.
