Кодовое дерево и решетчатая диаграмма
Еще одним очень наглядным способом описания и иллюстрации работы сверточных кодов является использование так называемого кодового дерева.
Рассмотрим сверточный (6.3)-код со схемой, изображенной на рис. 2.5.
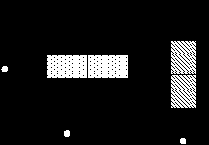
Рис. 2.5
Соответствующее этому кодеру кодовое дерево
– последовательность выходных состояний кодера при подаче на его вход цепочки входных символов 0 и 1 – приведено на рис. 2.6.
Рис. 2.6
На диаграмме рис. 2.6 изображены входные и выходные последовательности кодера: входные — направлением движения по дереву (вверх - 0, вниз - 1), выходные — символами вдоль ребер дерева. При этом кодирование состоит в движении вправо по кодовому дереву.
Например, входная последовательность m = (01000…… кодируется как U = (0011101100000… , последовательность m = (1010100000… - как U = (1110001000… .
Если внимательно посмотреть на строение приведенного на рис. 2.6 кодового дерева, можно заметить, что начиная с четвертого ребра его структура повторяется, т.е. каким бы ни был первый шаг, начиная с четвертого ребра значения выходных символов кодера повторяются. Одинаковые же узлы могут быть объединены, и тогда начиная с некоторого сечения размер кодового дерева перестанет увеличиваться.
Другими словами, выходная кодовая последовательность в определенный момент перестает зависеть от значений входных символов, введенных в кодер ранее.
Действительно, из рис. 2.6 видно, что, когда третий входной символ вводится в кодер, первый входной символ покидает сдвиговый регистр и не сможет в дальнейшем оказывать влияния на выходные символы кодера.
С учетом этого неограниченное кодовое дерево, изображенное на рис. 2.6, переходит в ограниченную решетчатую диаграмму (кодовое дерево со сливающимися узлами) рис. 2.7.
 Рис. 2.7 |
Кодирование сверточными кодами с использованием решетчатой диаграммы, как и в случае с кодовым деревом, представляет собой чрезвычайно простую процедуру: очередные символы входной последовательности определяют направление движения из узлов решетки: если 0, то идем по верхнему ребру, если 1 - по нижнему ребру. Однако в отличие от кодового дерева решетчатая диаграмма не разрастается по ширине с каждым шагом, а имеет начиная с третьего сечения постоянную ширину.
В качестве примера закодируем с помощью решетчатой диаграммы несколько информационных последовательностей.
Пусть m=(0110000… .
Соответствующая ей кодовая последовательность будет иметь вид:
U = (001101011100… ,
или m = ( 110100… , тогда
U = (1101010010110000…;
или m = ( 000000… , тогда
U = (1101010010110000
и т.д., проще не придумаешь.
