Закон Ома
Закон Ома для участка цепи: ток в проводнике I равен отношению падения напряжения U на участке цепи к ее электрическому сопротивлению R:
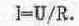
Закон Ома иллюстрируется схемой на рис. 5.1, из которой видно, что на участке цепи с сопротивлением R=100 Ом создается падение напряжения U=9,09 В, измеряемое вольтметром. Согласно (5.3) ток в цепи 1=9,09/100=90,9 мА, что и измеряет последовательно включенный в цепь амперметр. Отметим, что в рассматриваемой схеме внутреннее сопротивление амперметра выбрано равным 10'12 Ом, т.е. очень малым, а входное сопротивление вольтметра — 1012 Ом, т.е. очень большим, чтобы подключение измерительных приборов к цепи не оказывало сколько-нибудь заметного влияния на результаты измерений.
Отметим назначение ключей К и Х на рис. 5.1, управляемых нажатием одноименных клавиш клавиатуры. При размыкании ключа Х в схеме реализуется режим холостого хода, при этом вольтметр U измеряет ЭДС источника Е=10 В, а вольтметр Ui имеет нулевые показания. При замыкании ключа К в схеме реализуется режим короткого замыкания и, согласно (5.1), ток короткого замыкания Io=E/Ri=10/10=l А. При этом вольтметр Ui измеряет падение напряжения Ui=Io-Ri=10 В.
Закон Ома для полной цепи: ток в замкнутой электрической цепи равен ЭДС источника Е, деленной на сопротивление всей цепи. Применительно к цепи на рис. 5.1 ее полное сопротвление равно Ri + R, и на основании закона Ома получаем I=E/(Ri+R)=90,9 мА, что и измеряет амперметр.
Отметим, что на дисплее амперметра отображаются только три старшие разряда измеряемой величины, так что результат измерения округляется.
Обобщенный закон Ома [35]: ток в замкнутой одноконтурной цепи равен отношению алгебраической суммы всех ЭДС к арифметической сумме всех сопротивлений. Перед расчетом выбирают направление обхода контура и считают это направление за положительное направление тока. При определении алгебраической суммы ЭДС со знаком плюс берут те ЭДС, направления которых совпадают с выбранным положительным направлением тока, и со знаком минус — ЭДС с противоположными направлениями.
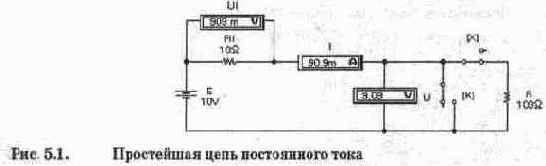
В качестве примера рассмотрим изображенную на рис. 5.2 одноконтурную цепь, состоящую из источников напряжения Е1=120 В, Е2=40 В и резисторов с сопротивлениями R1=12 Ом и R2=8 Ом. Определим напряжение между точками А и В.
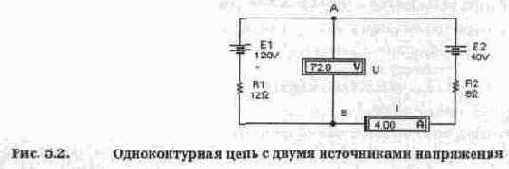
Выберем направление обхода контура по часовой стрелке. В таком случае ЭДС Е1 войдет со знаком "+", поскольку ток от Е1 совпадает с направлением обхода (положительным направлением тока во внешней цепи считается направление от положительного к отрицательному зажиму источника). При обходе же ветви с источником Е2 направление обхода не совпадает с направлением тока, который создается этим источником. Поэтому для схемы на рис. 5.2 ток в цепи 1=(Е1-E2)/(R1+R2)=80/20=4 А. Так как величина тока получилась положительной, то, следовательно, направление тока совпадает с выбранным. Если бы результат получился отрицательным, то это означает, что действительное направление тока в цепи противоположно выбранному.
Напряжение и.ь между точками А и В определяется с помощью закона Ома для участка цепи. Выберем участок А-Е2-В. Для этого участка закон Ома запишется в следующем виде:
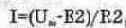
откуда
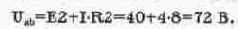
Контрольные вопросы и задания
1. Сформулируйте закон Ома для участка цепи. Чем он отличается от закона Ома для полной цепи?
2. Что представляет собой режим холостого хода и режим короткого замыкания?
3. Для схемы на рис. 5.1 проведите моделирование режимов холостого хода и короткого замыкания и сравните полученные результаты с расчетными.
4. Рассчитайте напряжение между точками А и В в схеме на рис. 5.2, используя ветвь В-Е1-А. Обратите внимание на порядок обхода участка цепи.
5. Проведите моделирование схемы на рис. 5.2, уменьшив ЭДС источников Е1 и Е2 в 4 раза.
6. Дополните цепь на рис. 5.3 необходимыми для моделирования измерительными приборами. Рассчитайте ток в цепи и падение напряжения на участке А-В. Сравните полученные результаты с результатами моделирования. Напомним, что на графическом обозначении батареи положительный зажим источника напряжения более широкий, чем отрицательный.

Метод контурных токов
Метод контурных токов (метод Максвелла) напоминает метод расчета с использованием законов Кирхгофа, однако он несколько проще и поэтому получил большее распространение на практике при расчетах многоконтурных цепей, состоящих из п независимых контуров. Определение токов в ветвях сводится к решению системы n=p-q+l уравнений для контурных токов 1ц,, 1гц 1эь...; действительный же ток в каждой ветви находится как алгебраическая сумма контурных токов, протекающих через соответствующую ветвь. Выбор направлений контурных токов произволен. Каждая из ветвей сложной электрической цепи должна войти хотя бы в один из анализируемых контуров.
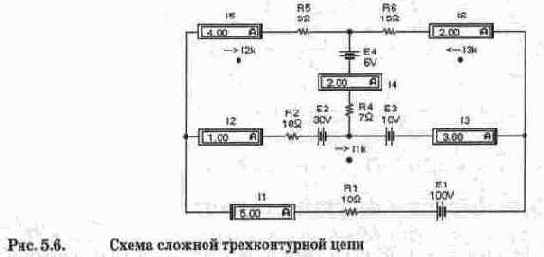
Для иллюстрации рассматриваемого метода расчета обратимся к схеме на рис. 5.6, на которой выбранные направления контурных токов обозначены стрелками, токи в ветвях контуров — расположением входных зажимов амперметров.
Составим систему уравнений для контуров:
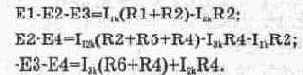
После подстановки числовых значений получим:
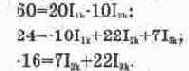
Решив эту систему уравнений, найдем контурные токи:
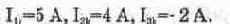
Теперь найдем истинные токи во всех ветвях. В ветви, где действует ЭДС Е1, истинный ток II имеет направление контурного тока 1ц и равен ему: 11=1ц=5 А. В ветви с сопротивлением R5 истинный ток 15 имеет направление контурного тока 1ц и равен ему: I5=l2k=4 А. В ветви с сопротивлением R6 истинный ток 16 имеет направление, противоположное контурному току laic, и равен 16=-1зь=2 А. В ветви с сопротивлением R2 истинный ток 12 получится наложением контурных токов 1ц и Izi, и будет иметь направление большего из них, т.е. I2=Iik-l2],=l А. В ветви с сопротивлением R4 истинный ток 14 получится наложением контурных токов 1ц, и 1эк и будет иметь направление большего из них, т.е. 1^1ц+1ц,=4+(-2)=2 А. В ветви, где действует ЭДС ЕЗ, истинный ток 13 получится наложением контурных токов 1ц и Igk и будет иметь направление тока Iik, т.е. 13=^+1з^5+(-2)=3 А. Из сравнения полученных расчетных данных с показаниями приборов на рис. 5.6 видно, что они полностью совпадают.
Контрольные вопросы и задания
1. В чем заключается отличие метода контурных токов от метода расчета с использованием законов Кирхгофа для аналогичных целей?
2. Выполните расчет токов' в ветвях схемы на рис. 5.6 методом контурных токов при Е1=50 В, Е2=15 В, Е3=5 В и Е4=3 В. Сравните полученные данные с результатами моделирования.
3. Выполните расчет токов в ветвях схем на рис. 5.5 методом контурных токов.
Метод наложения
При методе наложения ток в любой ветви схемы рассчитывается как алгебраическая сумма токов, вызываемых в ней каждой ЭДС в отдельности. При этом предполагается, что при анализе воздействия одной ЭДС остальные ЭДС принимаются равными нулю и при расчетах учитываются только их внутренние сопротивления.
При использовании метода наложения потребуются некоторые навыки в преобразовании электрических цепей. Во всех случаях замена одних схем другими, им эквивалентными, не должна приводить к изменению токов и напряжений на участках цепи, не подвергшихся преобразованию. Наиболее распространенные и часто употребляемые преобразования цепей сводятся к следующим.
1. Замена последовательных сопротивлений одним эквивалентным. Эквивалентное сопротивление R цепи, состоящей из последовательно соединенных сопротивлений Ri, Rg.-.Rn, равно сумме этих сопротивлений:
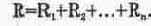
2. Замена параллельных сопротивлений одним эквивалентным. Сопротивления параллельны, если все они присоединены к одной паре узлов. Эквивалентное сопротивление R цепи, состоящей из ряда параллельно соединенных сопротивлений, определяется из формулы суммирования проводимостей:
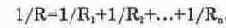
В случае двух параллельно соединенных сопротивлений
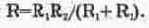
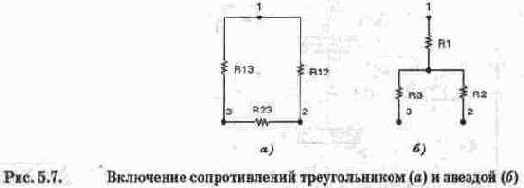
3. Преобразование треугольника сопротивлений (рис. 5.7, а) в эквивалентную звезду сопротивлений (рис. 5.7, б) и наоборот. Формулы преобразований имеют следующий вид:

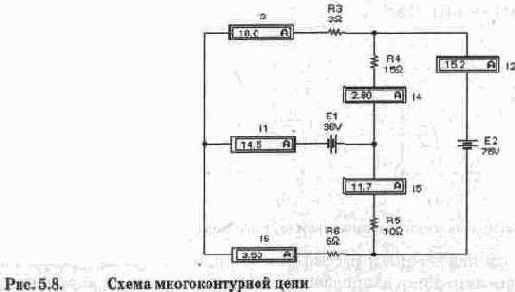
Вернемся к методу наложения и рассмотрим его применение для схемы на рис. 5.8. В этой схеме все источники напряжения идеальны, поэтому их внутренние сопротивления равны нулю. Предполбжим, что действует только ЭДС Е1, а вместо Е2 будет просто проводник (короткое замыкание). В этом случае ЭДС Е1 нагружена на эквивалентное сопротивление R„«,=R2-R6/(R3+R6)+R4-R5/(R4+R5)=8 Ом. При этом токи в ветвях составят:

Перейдем ко второму этапу, когда активной является ЭДС Е2, а Е1 — закоро-чена. В этом случае ЭДС Е2 нагружена на эквивалентное сопротивление R2,„=R3-R4/(R3+R4)+R5-R6/(R5+R6)=6,25 Ом. При этом токи в ветвях имеют следующие значения:
Складывая алгебраически токи, полученные от действия каждой ЭДС в отдельности, найдем истинные токи в каждой ветви:
что совпадает с результатами моделирования.
Контрольные вопросы и задания
1. Какие законы используются при расчете токов ветвей методом наложения?
2. Выполните расчет токов в ветвях схемы на рис. 5.8 методом наложения при Е1=48 В и Е2=45 В. Сравните полученные данные с результатами моделирования.
3. Выполните расчет токов в ветвях схем на рис. 5.5 методом наложения и проверьте результаты расчета путем моделирования.
Метод эквивалентного генератора
Метод эквивалентного генератора напряжения называют иногда методом короткого замыкания и холостого хода или методом активного двухполюсника. С его помощью определяется ток в определенной ветви схемы. Назовем ее АВ и предположим, что она содержит одно сопротивление R. Для нахождения тока в этой ветви размыкают ветвь и любым из рассмотренных выше методов определяют разность потенциалов и», на зажимах А, В разомкнутой ветви (режим холостого хода). Затем вычисляется сопротивление короткого замыкания R„„ равное эквивалентному сопротивлению остальной цепи. При этом имеющиеся в схеме источники должны быть выключены и заменены их внутренними сопротивлениями, а питание схемы осуществляется от постороннего источника, подключенного к зажимам А, В исследуемой ветви. Следующим этапом является режим короткого замыкания, при котором определяется ток 1„, в ветви АВ при закороченных зажимах А, В. Заметим, что этот этап не обязателен, если сопротивление Е„, удалось определить другим, более простым способом. Если же режим короткого замыкания все-таки пришлось применить, то в этом случае
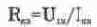
и искомый ток в ветви определяется из выражения:
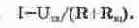
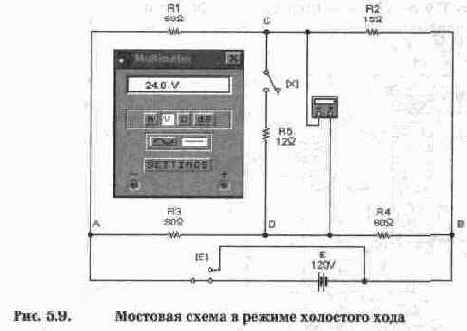
Перейдем к конкретному примеру. Для этого воспользуемся схемой на рис. 5.9, которая представляет собой мостовую схему из двух плеч, образованных резисторами Rl, R2, R3, R4. В одну диагональ моста включен идеальный источник напряжения Е и переключатель, управляемый клавишей Е клавиатуры. В другую диагональ моста включен резистор R5 с ключом X, который управляется одноименной клавишей. Нашей задачей является определение тока через резистор R5 в рабочем состоянии, когда ключ Х замкнут. В положении ключа X, показанном на схеме (ключ разомкнут), реализуется первый этап моделирования — режим холостого хода ветви CD. В этом режиме через сопротивления Rl, R2 протекает ток Г, а через сопротивления R3, R4 — ток I", которые равны соответственно
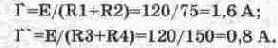
При этом потенциалы в точках С и D определяются падениями напряжений на резисторах Rl и R3:

Располагая потенциалами точек С и D, нетрудно найти и напряжение между ними, которое равно напряжению холостого хода:

что соответствует показаниям мультиметра на рис. 5.9.
Теперь найдем сопротивление короткого замыкания. Как отмечалось выше, сделать это можно двумя способами.
1. Путем непосредственного расчета с использованием данных схемы. В этом случае источник Е нужно выключить, оставив его внутреннее сопротивление, равное в данном случае нулю. Сопротивление короткого замыкания будет равно сопротивлению цепи между точками С и D:
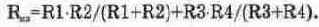
При моделировании на схеме рис. 5.9 необходимо ключ Е перевести в другое положение, а мультиметр — в режим омметра. Результаты таких действий показаны на рис. 5.10, откуда видно, что результаты проведенного расчета полностью подтверждаются результатами моделирования.
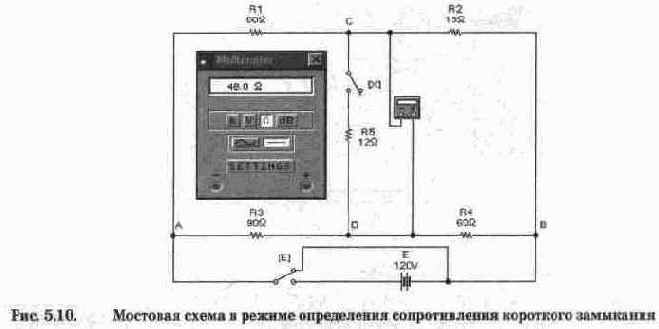
2. Искомое сопротивление можно найти и другим путем. Для этого нужно замкнуть точки С и D накоротко, вычислить ток 1,з, протекающий через короткозамк-нутый участок, и сопротивление короткого замыкания определить по формуле (5.6). Для моделирования такого режима необходимо ключ Е вернуть в исходное состояние, а мультиметр перевести в режим амперметра. Результаты моделирования показаны на рис. 5.11, из которого видно, что ток короткого замыкания равен 0,5 А. Тогда на основании формулы (5.6) R„,=24/0,5=48 Ом.
Теперь можно определить и искомый ток, используя формулу (5.7):
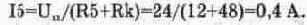
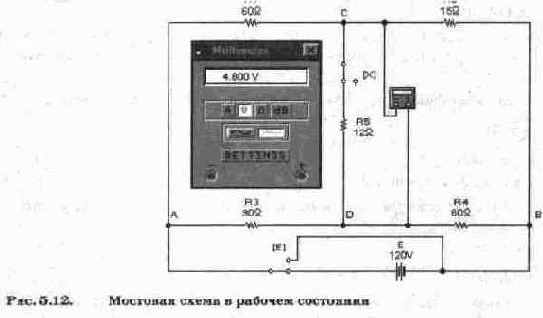
Для моделирования схемы в таком режиме ключ Х необходимо замкнуть, а мультиметр перевести в режим вольтметра. Результаты моделирования показаны на рис. 5.12, из которого видно, что падение напряжения на резисторе R5 равно 4,8 В, т.е. ток в цепи равен 4,8/12=0,4 А, что совпадает с расчетным значением.
Кроме метода эквивалентного генератора напряжения, существует также и метод эквивалентного генератора тока. Его применение основано на взаимных преобразованиях источника тока и источника напряжения с использованием формул (5.1) и (5.2). Метод эквивалентного генератора тока на практике нашел ограниченное применение, поэтому рассматривать его не будем.
Контрольные вопросы и задания
1. Какие законы теории цепей используются в методе эквивалентного генератора?
2. Проведите расчеты и моделирование рассмотренной мостовой схемы во всех режимах при сопротивлении резистора R5=6 Ом.
3. Рассчитайте ток через сопротивление R2 схемы на рис. 5.5, б методом эквивалентного генератора напряжения, сопровождая расчет моделированием.
Цепи постоянного тока
Реальные источники электрической энергии можно представить двояко:
1) в виде генератора напряжения, который характеризуется ЭДС Е, численно равной напряжению холостого хода и включенной последовательно с внутренним сопротивлением Ri;
2) в виде генератора тока, который характеризуется током I, численно равным току короткого замыкания реального источника, и параллельно подключенной проводимостью G¦.
Переход от генератора напряжения к эквивалентному генератору тока осуществляется по формулам:
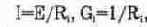
а обратный переход от генератора тока к эквивалентному генератору напряжения по формулам:
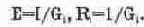
У идеального генератора напряжения внутреннее сопротивление R, равно нулю, а у идеального генератора тока равна нулю внутренняя проводимость G¦.
Рассматриваемые в этом разделе методы расчета цепей постоянного тока иллюстрируются примерами, большая часть которых взята из учебного пособия [35].
5.1. Закон Ома
5.2. Законы Кирхгофа
5.3. Метод контурных токов
5.4. Метод наложения
5.5. Метод эквивалентного генератора
Сложение колебаний
При сложении двух колебаний синусоидальной формы
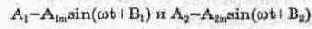
образуется синусоидальный сигнал той же частоты
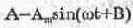
где
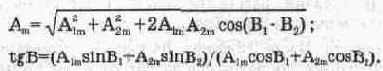
Следует заметить, что формула для А„ справедлива как для амплитудного, так и эффективного значения тока и напряжения, в чем нетрудно убедиться, подставив в эту формулу эффективные значения А,„и Аа„. Это замечание связано с тем, что далее мы будем пользоваться именно эффективными значениями токов, взятыми в данном случае из схемы на рис. 6.1.
Определим в качестве примера сумму и разность двух синусоидальных токов
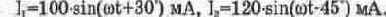
Используя приведенные выше формулы. лля СУММЫ токов ПОЛУЧИМ:

откуда фаза В=-10'10'.
Для вычисления разности токов воспользуемся соотношением:
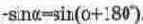
В этом случае вычитаемый ток
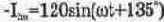
. Таким образом, задача вычитания второго тока из первого сводится к суммированию с учетом проделанных преобразований. Для разности токов в таком случае получим:
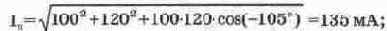
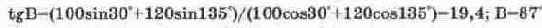
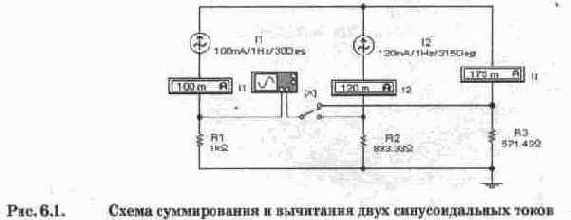
Схема для моделирования суммирования и вычитания синусоидальных токов показана на рис. 6.1. В ней использован источник переменного тока, в диалоговом окне которого можно задать частоту, ток и фазу в градусах. Однако задавать отрицательные значения фазы в программе не допускается. Поэтому для тока 12 задана начальная фаза 315°, поскольку sin(-45°)=sin(360°-45°). Для измерения токов в каждую ветвь включены амперметры в режиме измерения переменного тока (АС). Как видно из показаний амперметра, измеряющего ток Is, результаты суммирования токов совпадают с результатами расчетов.
Для измерения фазы использован осциллограф, в канале А которого регистрируется сигнал от источника II, создающий на резисторе R1 падение напряжение I1-R1=0,1-1000=100 В. Канал В осциллографа с помощью ключа Х может подключаться к резисторам R2, R3, сопротивления которых рассчитаны таким образом, чтобы токи II, Is создавали на них падения напряжения тоже 100 В (для удобства проведения осциллографических измерений). Пользуясь переключателем X, можно контролировать фазовые соотношения между токами II, 12, Is. В положении переключателя, показанном на рис. 6.1, такие соотношения можно регистрировать между токами II, Is.
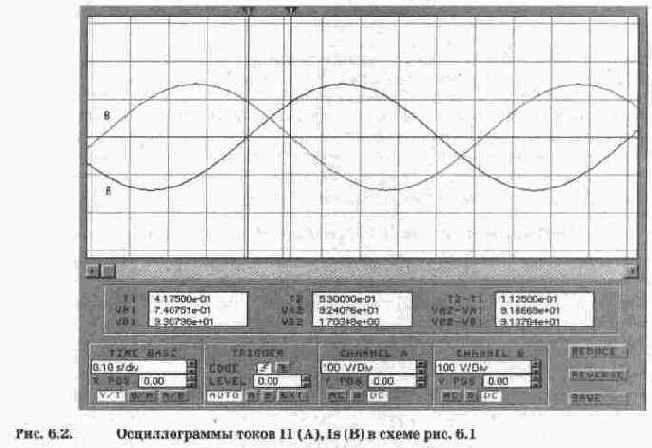
Результаты осциллографических измерений, полученные при моделировании процесса суммирования двух синусоидальных токов, показаны на рис. 6.2 (для повышения точности отсчета осциллограф включен в режиме ZOOM). Визирные линии поставлены в точки пересечения синусоидами оси времени (визирная линия 1 — для тока II, 2 — для тока Is). Из правого цифрового табло отсчетов видно, что временной промежуток между визирными линиями составляет Т2-Т1=0,1125 с. Поскольку период колебаний исследуемых сигналов составляет Т=1 с (частота 1 Гц), то измеренный промежуток времени, пропорциональный разности начальных фаз токов II, Is, в градусах может быть определен из очевидного соотношения:
В1-В=360°(Т2-Т1)/Т=360(0,1125)/1=40,5°=40°30', откуда фаза суммарного тока В=-10°30', что отличается от расчетного на 19'. Эта разница (около 3%) объясняется погрешностью отсчета временного интервала при установке визирных линий (так называемая погрешность параллакса).
Результаты моделирования вычитания токов приведены на рис. 6.3, откуда видно, что они полностью совпадают с данными расчета. Обратите внимание, в схе-
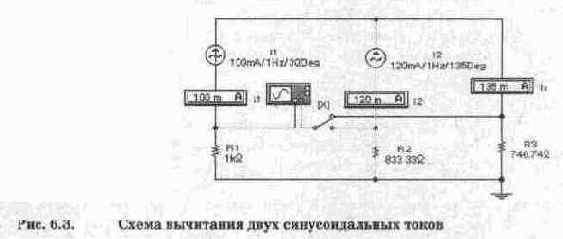
ме сопротивление резистора R3 изменено для удобства проведения осциллографических измерений.
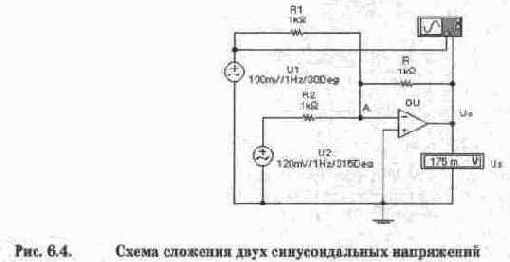
Рассмотрим теперь сложение напряжений
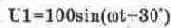
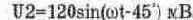
Схема измерений для этого случая показана на рис. 6.4. Она выполнена в виде суммирующего устройства на операционном усилителе OU. Коэффициент передачи для каждого источника напряжения равен R/R1=R/R2=1 (см. гл. 10). По существу с помощью суммирующего усилителя процесс сложения напряжений сведен к процессу суммирования токов I1=U1/R1 и I2=U2/R2 на резисторе R. При этом справедливость приведенных формул обеспечивается тем, что потенциал точки А за счет большого коэффициента усиления ОУ практически равен нулю.
Контрольные вопросы и задания
1. Почему методы расчета цепей постоянного тока нельзя использовать для расчета цепей переменного тока? В каких случаях это можно делать?
2. Проведите расчеты и моделирование сложения двух синусоидальных токов при разности фаз токов 60°.
3. Проведите анализ фазовых соотношений в схеме на рис. 6.3 по результатам моделирования.
4. С помощью осциллографа измерьте фазу суммарного напряжения в схеме на рис. 6.4.
Законы Ома, и Кирхгофа.
Второй закон Кирхгофа для мгновенных значений напряжений и тока в одноконтурной цепи (см. рис. 6.5), состоящей из последовательно соединенных активного сопротивления R, индуктивности L и емкости С, описывается выражением:
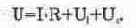
Из показаний приборов на рис. 6.5 видно, что в отличие от одноконтурной цепи постоянного тока, при арифметическом суммировании слагаемых правая и левая часть формулы (6.1) существенно отличаются друг от друга, т.е. U^U,+Ui+Uc. Объясняется это, как было показано в предыдущем разделе, наличием разности фаз суммируемых сигналов.
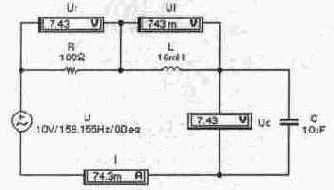
Рис. 6.5. Последовательная RLC-цепь
В курсе по теоретическим основам электротехники показывается [50], что если к источнику синусоидального напряжения
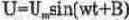
подключена последовательная RLC-цепь, по ней течет ток
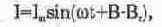
где
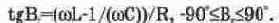
При этом принято называть:
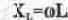
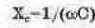
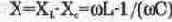
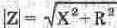
Контрольные вопросы и задания
1. Почему в схеме на рис. 6.5 выбрано такое странное значение частоты — 159,155 Гц?
2. С помощью формулы (6.2) рассчитайте значение амплитуды тока в цепи на рис. 6.5 и сравните полученные результаты с показаниями амперметра.
Индуктивность и емкость в цели переменного тока.
Для более глубокого понимания процессов, происходящих в последовательной RLC-цепи, целесообразно рассмотреть последовательные RL- и RC-цепи.
Для последовательной RL-цепи (рис. 6.6), выражения (6.2) и (6.3) имеют следующий вид:
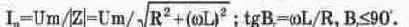
Модуль полного сопротивления RL-цепи при указанных на рис. 6.6 параметрах компонентов на частоте
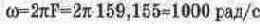
равен

Амплитуда и фаза тока:
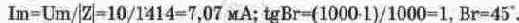
Падения напряжения на сопротивлении и индуктивности
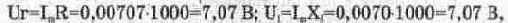
что совпадает с показаниями приборов на рис. 6.6.
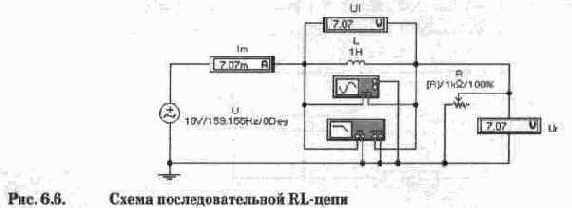
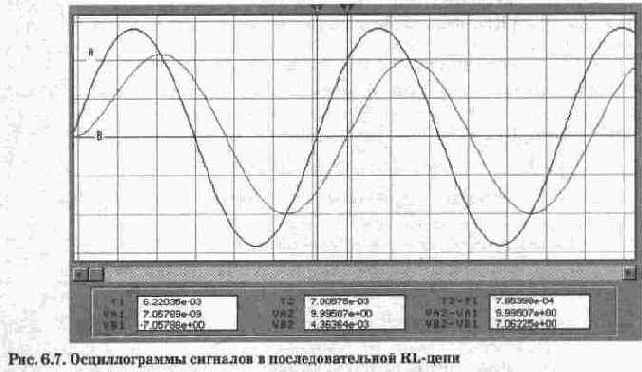
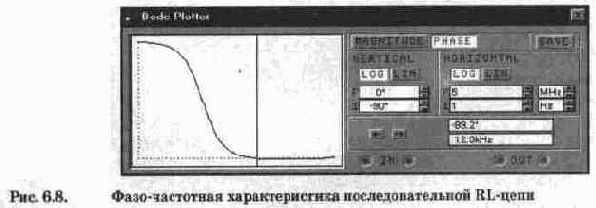
Для определения фазовых соотношений рассмотрим осциллограммы на рис. 6.7, откуда видно, что напряжение на входе RL-цепи (осциллограмма А, визирная линия 1) опережает напряжение на сопротивлении R (осциллограмма В, визирная линия 2) и, соответственно, ток в цепи на время Т2-Т1=0,000785 с. Поскольку период колебаний в данном случае равен 1/159,155=0,0063 с, то в градусах этот временной промежуток составит (360°-0,000785)/0,0063=44,98°, т.е. погрешность моделирования менее 0,05%. Заметим, что с повышением частоты этот угол стремится к 90°, что удобно наблюдать с помощью измерителя АЧХ-ФЧХ в режиме PHASE (режим ФЧХ). Результаты измерений показаны на рис. 6.8, откуда видно, что уже на частоте 12 кГц (в этой точке стоит визирная линия) ток в RL-цепи запаздывает относительно напряжения на ее входе более, чем на 89°.
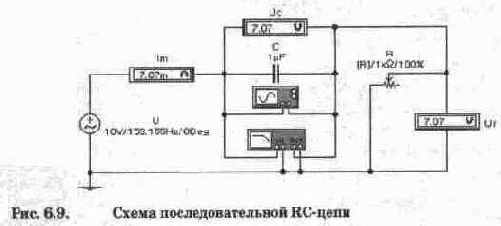
Для последовательной RC-пепи (рис. 6.9) из выражений (6.2) и (6.3) получаем:
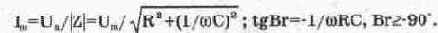
Контрольные вопросы и задания
1. Проведите расчет модуля и фазы тока в RC-цепи на рис. 6.9 и сравните полученные данные с результатами моделирования, приведенными на рис. 6.9. Обратите внимание на то, что в последовательной RC-цепи ток опережает входное напряжение в предельном случае на 90°. Следовательно, напряжения на емкости и индуктивности в RLC-цепи на рис. 6.5 могут быть сдвинуты по фазе на 180°, чем и объясняется тот факт, что индуктивное и емкостное сопротивления входят в формулу (6.2) с разными знаками.
2. Почему при расчетах фазовый угол В, имеет положительное значение для индуктивности и отрицательное для емкости, в то время как при моделировании результаты получаются противоположными? При поиске ответа рекомендуем обратить внимание на общее выражение для формул (6.2) и (6.3).
3. Проведите расчеты модуля и фазы тока в схемах на рис. 6.6 и 6.9 при частоте входного сигнала 1591,55 Гц. Результаты расчета сравните с результатами моделирования.
4. Составьте уточненные формулы для расчета коэффициента передачи делителей на рис. 4.46 и 4.47 (разд. 4.5).
Резонансные цепи
Явление, при котором индуктивное и емкостное сопротивления в RLC-цепи равны, называется резонансом.
Различают последовательный (для последовательной RLC-цепи) и параллельный (для параллельной RLC-цепи) резонанс. Последовательную RLC-цепь чаще всего называют последовательным колебательным контуром, а параллельную RLC-цепь — параллельным колебательным контуром. В случае малых потерь (сопротивление R пренебрежимо мало) для обоих контуров резонанс наступает при условии

откуда получается широко известное выражение для резонансной частоты;
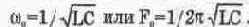
При последовательном резонансе (для последовательного контура) ток в цепи на рис. 6.5 определяется только сопротивлением R и совпадает по фазе с напряжением входного сигнала. При этом ток в цепи равен I„=U„/R и напряжения на индуктивности LT¦ и конденсаторе Uc
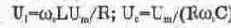
могут превышать напряжение входного сигнала в Q раз. Безразмерная величина

называемая добротностью, показывает, во сколько раз напряжение на индуктивности или емкости при резонансе превышает входное напряжение контура. На практике используется также величина, обратная добротности, которая называется коэффициентом затухания d=l/Q. Из (6.6) видно, что добротность контура возрастает с увеличением индуктивности L и уменьшением сопротивления потерь R и емкости С контура.
С учетом (6.4) выражение (6.6) может быть записано также в виде Q=W/R, где
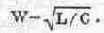
Параметр W имеет размерность сопротивления и называется характеристическим сопротивлением контура.
Амплитудно-частотная характеристика резонансной цепи определяется как отношение тока, определяемого выражением (6.2), к току при резонансе, т.е.
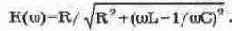
В радиотехнике зависимость, описываемую выражением (6.8), обычно называют резонансной кривой и для малых отклонений частоты относительно резонансной частоты используют для нее приближенное выражение:
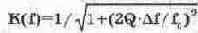
где

Приведем пример расчета последовательной RLC-цепи (рис. 6.10). Согласно (6.4) при указанных на схеме значениях индуктивности и емкости
Значение тока в цепи I„,=U„¦/R= 1/1000=1 мА соответствует показаниям амперметра !„,.
Согласно (6.5) падение напряжения на индуктивности и емкости U,=1000 0,001 1=1 В, U^O.OOl/OOOO/lO6)^ В.
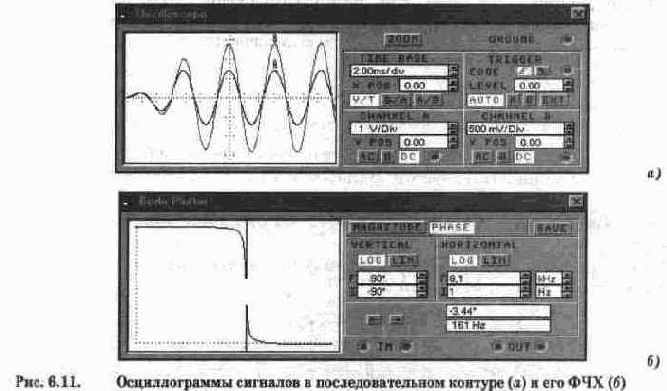
Осциллограммы сигналов в последовательном колебательном контуре показаны на рис. 6.11, а, из которого видно, что напряжение на сопротивлении (осциллограмма А) и, соответственно, ток в цепи совпадает по фазе с входным напряжением (осциллограмма В). Это означает, что на резонансной частоте фазо-частотная характеристика контура (рис. 6.11, б) должна иметь нулевое значение. Однако из-за дискретности визирная линия могла быть установлена на ФЧХ только вблизи резонансной частоты (161 Гц), поэтому значение фазы составляет 3,4°.
Рассмотрим резонанс токов в параллельной RLC-цепи. Наибольшее внимание резонансу этого типа уделяется в радиотехнике, где параллельный колебательный контур является основным элементом большинства частотно-избирательных устройств. В теоретических основах радиотехники показывается [51], что характеристики параллельного колебательного контура можно рассчитывать по формулам для последовательного контура. Однако имеются отличия, которые будут отмечены при рассмотрении конкретной схемы параллельного контура (рис. 6.12).
Собственно колебательный контур состоит из двух параллельно включенных ветвей: индуктивной с сопротивлением потерь в виде внутреннего сопротивления R¦ амперметра I, и емкостной с сопротивлением потерь в виде внутреннего сопротивления Re амперметра 1с. Напомним, что эти сопротивления могут изменяться и для рассматриваемой схемы установлены равными 1 Ом для обоих амперметров. К контуру подключены измерительные приборы, назначение которых очевидно; например, вольтметры U, и U,, предназначены для измерения падения напряжения на индуктивности L и на резисторе R.
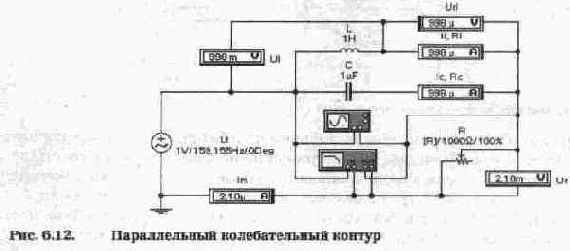
Для параллельного колебательного контура вводится параметр, который равен сопротивлению контура на резонансной частоте и называется резонансным сопротивлением Rp, определяемым по формуле:
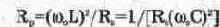
где R.=Rl+Rc — суммарное сопротивление потерь контура.
Соотношение между подводимым к контуру током 1„ и током в контуре Ii, на резонансной частоте определяется выражением:
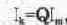
где Q определяется выражением (6.6), но с учетом того, что сопротивление потерь теперь обозначается как R.. Для схемы на рис. 6.12 имеем: Z„.=(1000 1)72=500000 Ом; Q=(1000 1)/2=500. Подводимый к контуру ток и ток контура: I„,=U/(Rp+R)=l/(500000-HOOO)=l,996 мкА; Ii,=l, 996-500=998 мкА, что практически совпадает с показаниями приборов. Имеющие место неточности определяются приближенностью используемых формул. Например, для параллельного контура точное значение резонансной частоты может быть определено из выражения:
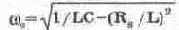
В случае пренебрежения сопротивлением R. выражение (6.11) совпадает с (6.4). Из (6.11) видно, что с увеличением потерь контура R. его резонансная частота уменьшается.
Амплитудно-частотная характеристика параллельного контура рассчитывается с помощью выражения (6.8). Для схемы на рис. 6.12 она имеет вид, показанный на рис. 6.13, а.
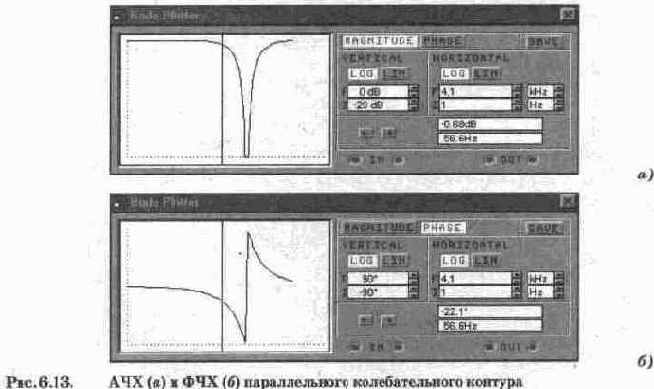
Фазо-частотная характеристика параллельного колебательного контура рассчитывается с помощью выражения (6.3) и показана на рис. 6.13, б.
Поскольку для практических применений наибольший интерес представляет область частот вблизи резонансной (в полосе
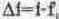
Из (6.12) видно, что при f=f„ фазовый угол равен нулю, однако уже при незначительном отклонении частоты в одну или другую сторону от резонансной будет наблюдаться резкое изменение фазы как в область отрицательных (при f<f„) так и положительных значений (при f>f„). Причем, крутизна переходного участка тем больше, чем больше добротность контура, а его ширина определяется отношением f„/Q, определяющем полосу пропускания
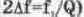
Контрольные вопросы и задания
1. Дайте определения явления резонанса в электрических цепях переменного тока и назовите условия его возникновения. В каких областях техники резонансные явления находят наибольшее применение?
2. Для схемы на рис. 6.12 проведите расчеты и моделирование при сопротивлениях потерь Rl=Rc=8 Ом. Уточните значение резонансной частоты с помощью соотношения (6.11).
3. Используя формулы (6.8), (6.3) и значения параметров на рис. 6.12, рассчитайте амплитудно-частотную и фазо-частотную характеристики и сравните полученные результаты с данными моделирования, приведенными на рис. 6.13.
Цепи переменного тока
В этой главе рассмотрим простейшие цепи переменного тока, иллюстрируя их примерами, частично заимствованными из учебного пособия [35].
Приведем перечень основных параметров переменного тока. 1. Мгновенное значение синусоидального сигнала:
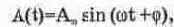
где t — текущее время; А„ — амплитуда; (р — начальная фаза; со — угловая частота. Период Т, угловая частота со и циклическая частота F связаны соотношениями:
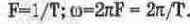
2. Действующие (эффективное) значения синусоидального тока и напряжения:
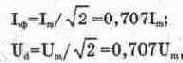
где I„, U„, — амплитуды тока и напряжения.
3. Средние значения синусоидального тока и напряжения за положительную полуволну:
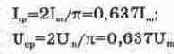
Среднее значение синусоидально изменяющейся величины на целом периоде равно нулю.
6.1. Сложение колебаний
6.2. Законы Ома, и Кирхгофа.
6.3. Индуктивность и емкость в цели переменного тока.
6.4. Резонансные цепи
Базовые усилительные каскады
Основные схемы построения усилителей на биполярных транзисторах определяются возможными способами их включения — ОБ, ОЭ и ОК, кратко рассмотренными в гл. 4; базовые схемы усилителей со вспомогательными элементами показаны на рис. 7.1.
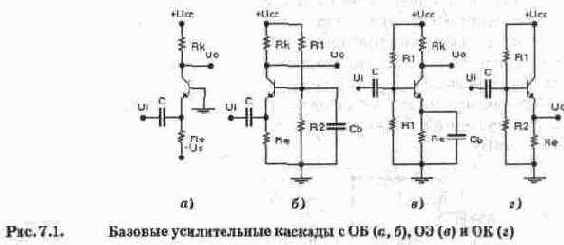
На рис, 7.1 обозначено: Ucc — напряжение питания, Ui — входное напряжение, Uo — выходное напряжение, Rk — сопротивление коллекторной нагрузки, С — разделительный конденсатор. Re — эмиттерное сопротивление, Rl, R2 — резисторы делителя, задающего режим каскада по постоянному току.
Особенностью классической схемы каскада с ОБ (рис. 7.1, а) является наличие отдельного источника смещения Us, с помощью которого задается режим транзистора по постоянному току, что достаточно неудобно. Поэтому на практике используется каскад ОБ по схеме рис. 7.1, б, в котором режим по постоянному току задается делителем на резисторах Rl, R2, а по переменному току база соединена с "землей" через блокировочный конденсатор СЬ.
Базовые каскады характеризуются входным R„ и выходным R,„, сопротивлением, коэффициентом усиления тока К, и напряжения К„. Ниже в качестве справочной информации приводятся приближенные выражения для этих характеристик.
Для каскада с ОБ:

Для каскада с ОЭ:
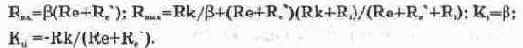
Для каскада с ОК:
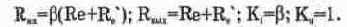
В приведенных формулах R,' — объемное сопротивление эмиттерного перехода; а — коэффициент усиления тока транзистора в схеме с ОБ; ¦¦ — значок параллельного соединения резисторов; R, — внутреннее сопротивление источника входного сигнала с учетом сопротивлений параллельно включенных резисторов Rl, R2; Р — коэффициент усиления тока транзистора в схеме ОЭ. Заметим, что каскады ОБ и ОК сигнал не инвертируют, а ОЭ — инвертирует. .
Проектирование усилителя начинается с определения режима транзистора по постоянному току, который называют статическим режимом.
В зависимости от тока коллектора транзистора и величины падения напряжения на электродах транзистора усилительного каскада, а также от амплитуды входного сигнала различают следующие режимы усиления: режим А; режим В; режим С; режим D и промежуточные режимы, например, АВ.
В режиме А ток в выходной цепи усилителя протекает в течение всего периода сигнала. Для иллюстрации обратимся к рис. 7.2, на котором показан каскад по схеме с ОЭ. В схеме использованы индикаторные вольтметры для контроля напряжений на электродах транзистора в статическом режиме, а также функциональный генератор и осциллограф для моделирования режима усиления. В программе EWB для рассматриваемой схемы нельзя отключить функциональный генератор, поэтому при моделировании статического режима установим минимальную амплитуду сигнала (в нашем случае 1 мкВ).
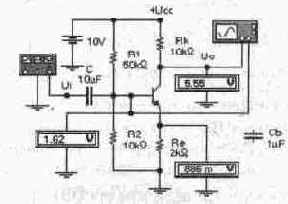
Рис. 7.2. Усилительный каскад по схеме с ОЭ
Для усилительного каскада класса А расчет статического режима заключается в выборе такого коллекторного тока 1„ (его называют током покоя или током в рабочей точке), при котором падение напряжения на коллекторной нагрузке Rk, во-первых, равно падению напряжения на транзисторе (напряжение коллектор-эмиттер U„) и, во-вторых, было бы меньше амплитудного значения при максимальном входном сигнале. Первое условие применительно к схеме на рис. 7.2 запишется следующим образом:
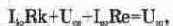
где
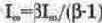
Поскольку В»1 (в рассматриваемом примере ), то
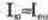
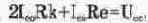
, откуда находим ток покоя
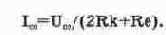
Рассмотрим теперь базовую цепь транзистора. Напряжение на базе относительно общей шины (с учетом того, что
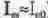
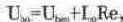
где Ubo, — напряжение база-эмиттер (для кремниевых транзисторов оно находится в пределах 0,7...0,9 В).
Поскольку Ubo равно падению напряжения на резисторе R2, ток через него равен
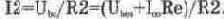
Через резистор R1 протекает сумма тока базы, равного 1„/р, и тока 12. Падение напряжения на резисторах R1, R2 равно напряжению питания Ucc. Поэтому для базовой цепи:
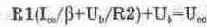
Если руководствоваться требованиями высокой термостабильности каскада (см. ниже), то необходимо выбирать
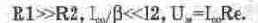
В таком случае с учетом (7.2) и (7.3) из (7.4) получаем выражение для ориентировочного расчета сопротивлений резисторов схемы с ОЭ:
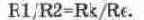
Подставляя в формулу (7.6) значения сопротивлений резисторов, используемых в схеме на рис. 7.2, убеждаемся в справедливости этого соотношения. При этом, как следует из показаний вольтметров, падение напряжения на коллекторном сопротивлении составляет 10-5,55=4,45 В и близко к значению падения напряжения на транзисторе 5,55-0,886=4,67 В, что соответствует первому условию обеспечения режима А.
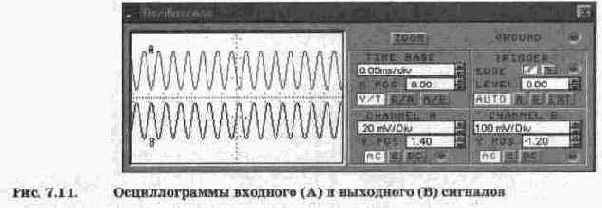
Коэффициент усиления каскада с ОЭ рассчитывается по приближенной формуле K„=Rk/Re (если Re не.зашунтировано емкостью). В рассматриваемом примере он равен 5. Следовательно, при амплитуде выходного напряжения 4,5 В (второе условие обеспечения режима А) на вход усилителя можно подать сигнал с амплитудой 4,5/5=0,9 В.
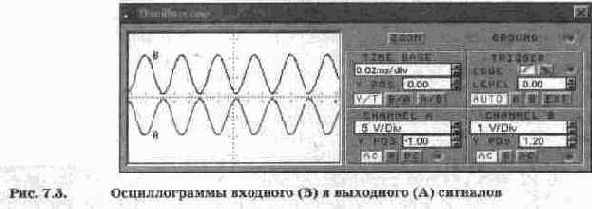
Осциллограммы входного и выходного сигналов показаны на рис. 7.3. Обращаем внимание на то, что оба канала работают в режиме АС и осциллограммы разнесены на экране с помощью смещения по вертикали (Y POS). Из осциллограмм видно, что выходной сигнал (осциллограмма А) по форме повторяет входной сигнал (осциллограмма В). Таким образом, достоинством режима класса А является минимум нелинейных искажений. Его недостатком является низкий КПД, меньший 0,5, поэтому он используется чаще всего в каскадах предварительного усиления, а также в маломощных выходных каскадах.
В режиме В ток через транзистор протекает в течение примерно половины периода входного сигнала (180°). Половину этого угла, соответствующего моменту прекращения тока через активный элемент, называют углом отсечки. В идеале этот угол равен 90°. Из-за нелинейности начальных участков характеристик транзисторов форма выходного тока при его малых значениях существенно отличается от формы тока в линейном режиме. Это вызывает значительные нелинейные искажения выходного сигнала.
Режим В обычно используют в двухтактных выходных каскадах, имеющих высокий КПД, в других каскадах его применяют сравнительно редко. Чаще выбирают промежуточный режим АВ, при котором угол отсечки несколько больше 90° и при отсутствии входного сигнала через активный элемент протекает ток, равный 5...15% от максимального тока при заданном уровне входного сигнала. Такой выбор позволяет уменьшить нелинейные искажения.
В режиме С ток через транзистор протекает в течение промежутка времени, меньше половины периода входного сигнала, т.е. при угле отсечки меньше 90°. Ток покоя в режиме С равен нулю. Его используют в мощных усилителях, в которых нагрузкой является резонансный контур (например, в выходных каскадах радиопередатчиков).
Режим D (или ключевой) — режим, при котором транзистор находится только в двух состояниях: или полностью заперт, или полностью открыт. Такой режим используется в ключевых схемах, о которых речь пойдет в следующей главе.
При выборе параметров рабочей точки активного элемента необходимо учитывать разброс его параметров от экземпляра к экземпляру и их зависимость от температуры (обратный ток переходов, коэффициент передачи по току), а также подверженность изменению во времени (за счет старения). Все это требует принятия специальных мер для стабилизации коэффициента усиления и других параметров усилителей.
Изменения параметров особенно опасны в первых каскадах усилителей постоянного тока, так как при гальванической межкаскадной связи и большом коэффициенте усиления это может привести к существенному изменению нулевого уровня на выходе. Поэтому в большинстве транзисторных усилителей для стабилизации положения рабочей точки вводят стабилизирующую обратную связь или используют методы температурной компенсации (в частности, введением термозависимых сопротивлений).
Для оценки влияния температуры на параметры усилительных каскадов используется коэффициент температурной нестабильности S,=p/[l+pYi,], где Yb=Re/(Re+Rb), Еь — сопротивление базового делителя (для схемы на рис. 7.2 оно равно сопротивлению параллельно включенных резисторов Rl, R2). Максимальная температурная стабильность статического режима обеспечивается при Уь=1. Следовательно, для повышения температурной стабильности желательно выполнение условия Re»Rb, т.е. она будет тем лучше, чем больше сопротивление в цепи эмиттера и чем меньше эквивалентное сопротивление делителя Rl, R2, задающего режим по постоянному току.
Для повышение температурной стабильности усилительных каскадов используют также различные способы термостабилизации.
Первый способ термостабилизации — параметрический — основан на применении термочувствительных элементов, в частности, полупроводниковых диодов (в схеме на рис. 7.2 это может быть диод, подключенный последовательно с резистором R2). При изменении температуры окружающей среды сопротивление термозависимого элемента изменяется так, что изменение тока базы или напряжения между эмиттером и базой компенсирует изменение тока коллектора. Очевидно, что характеристика такого термоэлемента должна обладать соответствующей температурной зависимостью. А так как это сделать трудно, то для обеспечения нужных характеристик в ряде случаев параллельно термоэлементу и последовательно с ним включают специальным образом подобранные активные сопротивления. Это усложняет схему, и, кроме того, с течением времени такая компенсация нарушается.
Второй способ термостабилизации — применение отрицательной обратной связи по постоянному току, причем используют как местную, так и общую обратные связи. При местной обратной связи чаще всего применяют обратную связь по току и несколько реже — обратную связь по напряжению. В схеме на рис. 7.2 применена обратная связь по току, сущность которой заключается в том, что делитель на резисторах R1, R2 задает потенциал базы и тем самым жестко фиксирует потенциал эмиттера. Так как этот потенциал обусловлен падением напряжения на резисторе Re, то тем самым задается ток эмиттера. При этом изменения параметров транзистора, изменяющие ток коллектора, изменяют соответствующим образом ток эмиттера и падение напряжения на резисторе Re. Это приводит к изменению разности потенциалов между базой и эмиттером. Ток базы при этом изменяется таким образом, что изменение тока коллектора будет в той или иной мере скомпенсировано.
Чем меньше эквивалентное сопротивление базового делителя, тем в меньшей степени потенциал базы зависит от изменений базового тока и тем лучше стабилизация. Но при малых сопротивлениях R1, R2 резко возрастает мощность, потребляемая от источника питания, и уменьшается входное сопротивление каскада.
Если необходимо иметь стабильный режим по постоянному току и максимальное усиление по переменному току, вводят достаточно глубокую обратную связь за счет увеличения сопротивления резистора Re, параллельно которому включается конденсатор большой емкости (конденсатор СЬ на рис. 7.2), которая определяется из условия: 2nF„„„CbRe»l, где F„i„ — минимальная частота сигнала.
В многокаскадных усилителях для стабилизации статического режима предпочтение отдается общей отрицательной обратной связи по постоянному току, охватывающей целиком весь усилитель. При этом местные обратные связи применять нецелесообразно, так как они всегда уменьшают коэффициенты усиления отдельных каскадов и снижают эффективность общей обратной связи.
Усилительные каскады на полевых транзисторах, в отличие от биполярных, управляются напряжением, приложенным или к запертому р—га-переходу (в транзисторах с управляющим р—га-переходом) или между электрически изолированным затвором и подложкой, которая часто соединяется с одним из электрбдов транзистора (в МДП-транзисторах). Ток затвора в усилительных каскадах на полевых транзисторах достаточно мал и для кремниевых структур с управляющим р—га-переходом не превышает 10 нА. Для МДП-транзисторов этот ток на несколько порядков меньше. Для транзисторов с р—га-переходом входное сопротивление на низких частотах составляет десятки мегом, а для МДП-транзисторов достигает десятков и сотен тера-ом. С повышением частоты входное сопротивление транзисторов существеннс уменьшается из-за наличия емкостей затвор-исток и затвор-сток.
Среди базовых каскадов на полевых транзисторах на практике наибольше( распространение получили каскады с общим истоком (аналог ОЭ) и истоковые повто рители (аналог ОК), показанные в двух модификациях на рис. 7.4 и отличающиеся способом реализации статического режима: смещение обеспечивается или за счет падения напряжения на резисторе, включенном в цепь истока (рис. 7.4, а, в), или за счет подачи на затвор дополнительного напряжения (рис. 7.4, б, г), Так как ток затвора полевых транзисторов весьма мал, можно считать, что в первом случае напряжение затвор-исток практически равно падению напряжения на сопротивлении Rs.
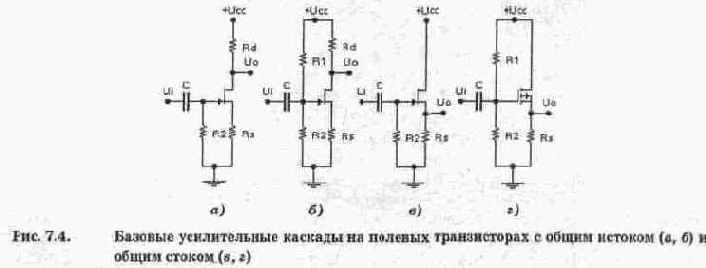
Для полевого транзистора с управляющим р—п-переходом, работающего в широком диапазоне температур, положение рабочей точки может изменяться из-за дополнительного падения напряжения на резисторе R2, сопротивление которого обычно выбирается достаточно большим. Это связано с изменением обратного тока р—п-перехода, выполняющего роль затвора, изменением контактной разности потенциалов затвор-канал и подвижности носителей заряда в канале. Изменение тока стока при фиксированном напряжении смещения определяется приближенным соотношением
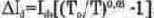
где 1д„ — ток стока при температуре Т„; Т — температура, для которой определяется
Анализ дестабилизирующих факторов, вызывающих изменение тока стока, показывает [12, 48], что при изменении температуры они имеют разные знаки и, следовательно, возможна их взаимная компенсация. Точка, в которой при изменениях температуры изменение тока стока минимально, называют температурно-ста-бильной точкой. Однако эффективная компенсация возможна только в небольшом диапазоне температур. При этом для полевых транзисторов с изолированным затвором температурно-стабильная рабочая точка отсутствует вообще.
Основным приемом повышения температурной стабильности является увеличение глубины последовательной обратной связи по току, что осуществляется за счет увеличения сопротивления Rs и, как следствие, сопровождается увеличением напряжения смещения. В итоге уже при сравнительно небольших напряжениях затвор-исток полевые транзисторы работают вблизи режима отсечки, где крутизна характеристики мала. Для устранения этого недостатка на затвор подают дополнительное отпирающее напряжение от делителя напряжения на резисторах R1, R2 (рис. 7.4, б, г), что обеспечивает работу транзистора на участке с большей крутизной.
У полевых транзисторов с индуцированным каналом подача напряжения смещения от внешнего источника обязательна, так как в его отсутствие транзистор заперт. Температурная стабилизация осуществляется за счет последовательной обратной связи, которая вводится с помощью резистора Rs.
Следует отметить, что температурные изменения тока стока в полевых транзисторах во много раз меньше изменений коллекторного тока биполярных транзисторов. Поэтому, как правило, обеспечение требуемой температурной стабильности не вызывает больших затруднений. Возникающая при этом обратная связь по переменному току нейтрализуется шунтированием резистора Rs блокировочным конденсатором.
При анализе усилительных каскадов на полевых транзисторах оперируют с крутизной характеристики S„ и током стока 1д„ которые соответствуют нулевому напряжению затвор-исток. При этом используют следующие приближенные соотношения, описывающие характеристики полевых транзисторов:
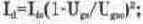
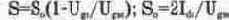
. В этих формулах I„ — текущее значение тока стока, I,», So — начальный ток стока и крутизна характеристики при напряжении отсечки U,„;
Ug„ S — текущие значения напряжения затвор-исток и крутизны.
Входное сопротивление усилительных каскадов на рис. 7.4 в области средних частот равно сопротивлению резистора R2 или R1¦¦R2, выходное сопротивление каскада с общим истоком равно Rd¦¦Ra.d, где R^ — дифференциальное сопротивление канала сток-исток; как правило, оно существенно больше Rd, поэтому выходное сопротивление практически равно Rd. Для каскада с общим стоком при выполняющихся на практике допущениях SRs» 1 и SR^ »1 выходное сопротивление равно 1/S. Коэффициенты усиления по напряжению каскадов с общим истоком и стоком определяются соответственно формулами:
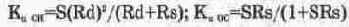
Схема для моделирования каскада с общим истоком приведена на рис. 7.5.
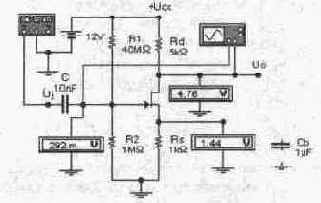
Рис. 7.5. Усилительный каскад с ОИ
Контрольные задания
1. По аналогии с рис. 7.2 составьте схему для исследования каскада с ОБ на рис. 7.1, б. Проверьте применимость полученных формул для каскада с ОЭ при определении параметров статического режима.
2. По аналогии с рис. 7.2 составьте схему для моделирования эмиттерного повторителя. При этом примите R1=R2, сопротивление этих резисторов выберите из условия малого влияния на входное сопротивление каскада (влияние минимально при бесконечном сопротивлении).
3. В схеме на рис. 7. 2 нейтрализуйте обратную связь по току на частотах выше 1 кГц путем подключения параллельно резистору Re блокировочного конденсатора СЬ. Измерьте коэффициент усиления на частоте 10 кГц. Необходимо учесть, что при этом коэффициент усиления напряжения на постоянном токе определяется формулой K„=Rk/Re', где Re'— омическое сопротивление эмиттера транзистора, задаваемое в перечне параметров транзистора.
4. В схеме на рис. 7.5 с помощью осциллографа определите коэффициент усиления и сравните его с результатами расчета по формуле (7.7). Исследуйте зависимость коэффициента усиления напряжения от сопротивлений резисторов Rd, Rs и крутизны транзистора (крутизна задается в редактируемом перечне параметров), а также от емкости блокировочного конденсатора СЬ, подключаемого параллельно резистору Rs. Обращаем внимание на необходимость установки соответствующего входного сопротивления вольтметра, контролирующего напряжение на затворе транзистора (по умолчанию оно равно 1 МОм, что явно мало).
Дифференциальный усилитель
Дифференциальный усилитель (ДУ) является одним из основных каскадов операционного усилителя. Простейший ДУ (рис. 7.6, а) состоит из двух одинаковых плеч, каждое из которых содержит транзистор и резистор нагрузки. Эмиттеры транзисторов соединены между собой и через резистор Re подключены к общей шине.
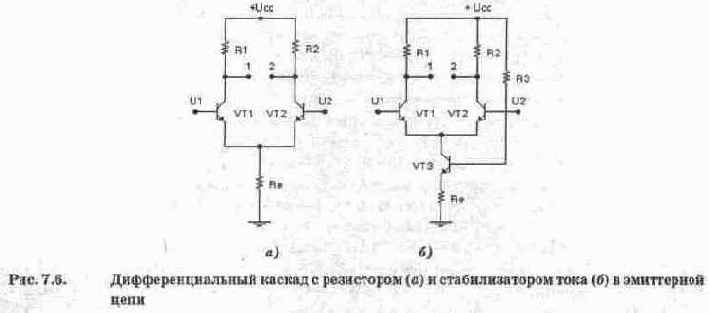
Предположим, что каскад абсолютно симметричен, т.е. сопротивления резисторов и параметры транзисторов, входящих в каждое плечо, одинаковы. Тогда при одинаковых входных сигналах U, и U; токи транзисторов также будут одинаковы, а это означает, что разность потенциалов между коллекторами (точки 1, 2) будет равна нулю. Этот случай, когда оба входных сигнала одинаковы как по амплитуде, так и по фазе, называется режимом усиления синфазного сигнала.
Если на оба входа подать одинаковые по уровню, но разные по фазе сигналы, то в результате ток одного транзистора увеличится, а другого на столько же уменьшится. В этом случае разность потенциалов между коллекторами будет пропорциональна удвоенному значению изменения напряжения на коллекторе транзисторов. При этом через резистор Re будет течь неизменный ток.
Если положительное приращение получит сигнал только на одном входе, например, на первом, это приведет к увеличению коллекторного тока транзистора VT1 и, следовательно, тока через резистор Re. Но увеличение падения напряжения на резисторе Re вызовет уменьшение разности потенциалов между базой и эмиттером транзистора VT2, и его ток уменьшится, причем изменение тока транзистора VT2 будет таково, что приращения напряжений эмиттер-база обоих транзисторов будут одинаковы. Следовательно, при увеличении входного напряжения на некоторую величину потенциал эмиттера увеличится на половину этой величины. При этом приращение напряжения база-эмиттер для обоих транзисторов будет одинаковым, но разного знака. Очевидно, что независимо от того, на какой вход каскада подаются напряжения, токи транзисторов меняются одинаково и приращения их вызваны половиной разности напряжений, приложенных между входами. Это дает основание при анализе дифференциального каскада рассматривать только одну его половину, считая, что к его входу приложено напряжение, равное половине разности напряжений на входах ДУ, а сопротивление в цепи эмиттера Re равно нулю.
Важной характеристикой ДУ является коэффициент подавления синфазного сигнала, который показывает, во сколько раз коэффициент усиления дифференциального входного сигнала, приложенного между входами каскада, больше коэффициента усиления синфазных сигналов, действующих между каждым входом и общей шиной (землей). Анализ показывает [12, 48], что для увеличения коэффициента подавления необходимо увеличивать сопротивление Re, Однако при этом приходится сталкиваться с проблемой обеспечения необходимого режима транзисторов по постоянному току. Трудности заключаются в необходимости увеличения напряжение питания до такой величины, что его реализация становится технически нецелесообразной. Кроме того, на резисторе Re при этом будет бесполезно рассеиваться электрическая мощность, что снижает КПД каскада.
Для устранения этого недостатка вместо резистора Re включают транзистор по схеме с ОЭ (рис. 7.1, б), который выполняет роль источника тока. Выходное сопротивление транзистора VT3 не равно бесконечности и примерно равно дифференциальному сопротивлению коллекторного перехода.
Хотя в идеальном дифференциальном каскаде синфазный входной сигнал не вызывает появления выходного сигнала, в реальном каскаде имеется небольшой выходной сигнал. Он обусловлен неполной идентичностью характеристик транзисторов, коллекторных нагрузок и внутренних сопротивлений источников входных сигналов.
В диапазоне высоких частот существенную роль в разбалансе каскада играют емкости коллекторных переходов. Они являются основной причиной роста усиления синфазного сигнала в диапазоне высоких частот.
Тот факт, что работа ДУ основывается на идентичности его плеч, объясняет популярность этих усилителей в микроэлектронике. Только в интегральных схемах, где .элементы расположены друг от друга на расстояниях десятков микрон, можно обеспечить полную идентичность параметров транзисторов.
Рассмотрим важнейший параметр ДУ — коэффициент усиления дифференциальной составляющей сигнала К, который часто называют просто коэффициентом усиления. Как отмечалось выше, ДУ может при анализе рассматриваться как каскад с ОЭ при Re=0. Следовательно, его коэффициент усиления определяется выражением [121:
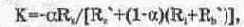
где Rk—Rl—R2; Re , Rb — объемные сопротивления эмиттера и базы соответственно;
R, — внутреннее сопротивление источников входного сигнала; (X — коэффициент усиления тока в схеме с ОБ.
Очевидно, что коэффициент усиления ДУ значительно больше, чем у каскада с ОЭ, поскольку Re=0 (для каскада с ОЭ коэффициент усиления обратно пропорционален R.'+Re). Следовательно, при гораздо меньшей нестабильности статического режима ДУ имеет гораздо больший коэффициент усиления что является его вторым важным преимуществом.
В случае источников сигнала с малым внутренним сопротивлением (R, менее 1 кОм) и небольших рабочих токах (менее 1 мА) вторым слагаемым в знаменателе вы-оажения (7.8) можно поенебоечь: тогда
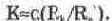
При а=0,9, R,=4 кОм и R.'=10 Ом из (7.9) получаем К=360.
При определении коэффициента усиления синфазной составляющей на оба входа ДУ подается входной сигнал от одного источника. При таком условии коэффициент усиления определяется как [12]
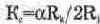
Следующий параметр ДУ — коэффициент подавления синфазной составляющей Кд, — характеризует влияние синфазной составляющей входного сигнала на дифференциальную составляющую выходного сигнала. Поскольку на практике синфазная составляющая входного сигнала может в тысячи раз превышать дифференциальную составляющую, то значение Кд, должно быть меньше К на несколько порядков. Соотношение модулей этих двух величин принято характеризовать коэффициентом подавления синфазной составляющей, выраженным в децибелах:
K„=201g¦K/KJ. Распространенным типом синфазного сигнала являются различные помехи (внутренние и внешние) и наводки, действующие одновременно на оба входа. Поэтому увеличение коэффициента К„ — один из основных путей повышения помехоустойчивости ДУ. Для оценки К„ используется выражение [12]:
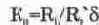
где 5=Act/a+ARk/Rk — коэффициент асимметрии ДУ, т.е. сумма относительных разбросов параметров его плеч; при необходимости эту сумму можно дополнить разбросом других параметров транзисторов.
Из выражения (7.11) следует важный вывод: коэффициент подавления синфазной составляющей находится в прямой зависимости от сопротивления источника сигнала R,. Следовательно, это сопротивление должно быть как можно больше.
Различают входные сопротивления ДУ для дифференциальной и синфазной составляющих сигнала, которые существенно различаются.
Входное сопротивление для дифференциальной составляющей равно удвоенному входному сопротивлению каждой половины ДУ и определяется выражением:
R,=2[(P+l)R.'+Rb']. Например, при (3=100, R,'=25 Ом и R„'=150 Ом R„=5,35 кОм. Поскольку сопротивление R,' обратно пропорционально току покоя 1„, то для увеличения входного сопротивления целесообразно использовать ДУ в режиме малых токов — в микрорежиме. Кроме того, целесообразно использовать транзисторы с высокими значениями (3, например, каскад Дарлингтона (см. ниже). Так, если 1„,=50 мкА и Р=2000, то R.'=0,5 кОм и R,=2 МОм.
Входное сопротивление для синфазной составляющей определяется сопротивлением источника тока R¦ в соответствии с выражением Rc=(p+l)Ri. Поскольку R,»Re', то Re намного превышает Рд.
Еще один параметр ДУ — динамический диапазон — характеризует отношение максимального и минимального напряжения входных сигналов, выраженное в децибелах. Минимальный сигнал ограничивается уровнем собственных шумов, а максимальный — нелинейными искажениями. Оценить максимально допустимый сигнал можно, например, следующим образом. Пусть в режиме покоя U,„=0,5Ucc. При положительной полярности входного сигнала потенциал V, уменьшается вплоть до нуля (после чего наступает насыщение транзистора), а при отрицательной полярности увеличивается вплоть до Ucc (после чего транзистор запирается). Таким образом, в обоих случаях максимальное приращение напряжение на коллекторе составляет 0,5Ucc. Деля эту величину на коэффициент усиления, получаем максимально допустимый входной сигнал.
Синфазные сигналы могут иметь гораздо большие амплитуды, чем дифференциальные, поскольку коэффициент К„ значительно меньше Кд. Обычно К.<1, поэтому синфазные входные сигналы могут составлять несколько вольт, вплоть до напряжений, близких к Ucc.
Неизбежная асимметрия плеч реальных ДУ является причиной того, что в режиме покоя имеется разность потенциалов между точками 1,2, которой соответствует на входе дифференциальный сигнал, называемый напряжением смещения нуля U„. Чтобы устранить разбаланс выходных потенциалов, нужно подать на вход дифференциальный сигнал, равный U„„ и имеющий противоположный знак. Напряжение смещения нуля состоит из нескольких слагаемых, каждое из которых зависит от разброса токов эмиттеров, коллекторных сопротивлений и др.
Разброс токов эмиттеров (при одинаковых напряжениях U.) обусловлен разбросом тепловых токов эмиттерных переходов: в транзисторе с меньшим током 1ц, будет меньше и ток 1е. Для того чтобы выровнять токи эмиттеров, на вход ДУ подается "выравнивающий" дифференциальный сигнал.
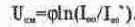
Например, если тепловые токи различаются на 20%, то U„„=5 мВ.
Вторая по важности составляющая напряжения смещения обусловлена разбросом коллекторных сопротивлений. Пусть токи в плечах одинаковы, тогда разность коллекторных потенциалов в режиме покоя составит:
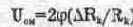
Например, при разбросе коллекторных сопротивлений 2% получаем U^=1 мВ. Другие составляющие, связанные с разбросом коэффициента а, сопротивления R.' и др., менее существенны.
Следует заметить, что напряжение смещения нуля зависит от температуры. Эта зависимость характеризуется температурной чувствительностью, измеряемой в мкВ/°С. Интересно, что температурная чувствительность уменьшается вместе с уменьшением напряжения смещения [12].
Кроме начального разбаланса коллекторных потенциалов, имеет место также начальный разбаланс входных токов 1„. Этот параметр называют током смещения или просто разностью входных токов. Влияние разности входных токов проявляется в том, что ток смещения, протекая через внутреннее сопротивление источника входного сигнала, создает на нем падение напряжения, которое равносильно появлению напряжения смещения. Например, если разность входных токов 20 нА и R,=100 кОм, то U,„=2 мВ.
Схема для исследования ДУ показана на рис. 7.7. По сравнению с рис. 7.1, б, она дополнительно содержит элементы задания статического режима (резисторы Els, R2s), блокировочный конденсатор СЬ в цепи питания, источники входного сигнала, внутренние сопротивления которых имитируются резисторами Ri, Ri', а также контрольно-измерительные приборы. С помощью вольтметров, подключенных к коллекторам транзисторов ДУ, можно измерять напряжения смещения при изменении сопротивлений резисторов RI, R2, Ri, Ri' и параметров транзисторов в статическом режиме и сравнивать полученные результаты с данными расчетов по формулам (7.12) и (7.13), а с помощью вольтметра в эмиттерной цепи транзистора VT3 —контролировать ток покоя по напряжению на резисторе Re. Изменяя фазу источников входных сигналов, можно имитировать чисто синфазные входные сигналы (фаза обоих источников выбирается одинаковой, амплитуда — не более напряжения питания Ucc), дифференциальные сигналы (параметры источников показаны на рис. 7.7), смешанный режим (фазы отличаются на несколько градусов, амплитуда — несколько меньше Ucc).
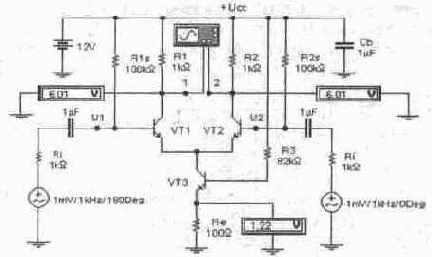
Рис. 7.7. Схема испытаний ДУ
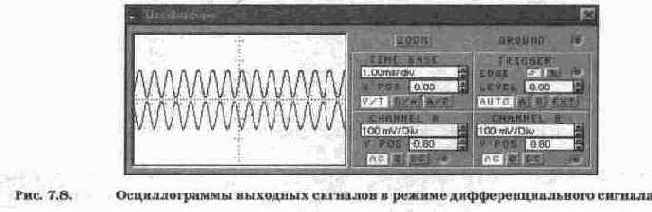
На рис. 7. 8 показаны осциллограммы выходных сигналов схемы на рис. 7.7, откуда видно, что амплитуда выходного напряжения составляет около 75 мВ (напомним, что точное значение можно получить в режиме ZOOM), что соответствует эффективному значению 53 мВ. Поскольку эффективное значение входного сигнала равно 1 мВ, коэффициент усиления равен 53. Расчет по формуле (7.8) при выбранных параметрах транзисторов (Re'=5 Ом, Ri,'=10 Ом, к=0,99) дает значение около 65, т.е. получается несколько завышенный результат, что объясняется неидеальностью источника тока на транзисторе VT3.
Для улучшения характеристик транзисторных ДУ используется ряд схемотехнических решений, в частности, широкое применение нашел каскад Дарлингто-на и более качественный стабилизатор тока (рис. 7.9).
Каскад Дарлингтона (рис. 7.9, а) относится к классу так называемых составных транзисторов, обладающих такими свойствами, которые трудно или невозможно получить в транзисторах с обычной структурой. Особенностью каскада Дарлингтона является исключительно большой коэффициент усиления тока базы, равный [12]: B=Bi+B2+BiBz, где Вц Bz — коэффициенты усиления тока транзисторов VT1 и VT2. Во всех практических случаях первые два члена в правой части приведенного выражения не существенны и эквивалентный коэффициент усиления можно записать в виде В=В1Вг.
Если составляющие В, и В; равны 100... 200, то коэффициент усиления тока В составит (I... 4)101. В практических схемах В1 может быть существенно меньше В2. Поэтому реальные значения коэффициента В составляют несколько тысяч, как и у транзисторов со сверхтонкой базой. Этот недостаток каскада Дарлингтона объясняется существенной разницей эмиттерных токов транзисторов. Для их выравнивания параллельно эмиттерному переходу транзистора VT2 включают резистор R (рис. 7.9, б), что позволяет достичь коэффициента усиления порядка 1000... 5000.
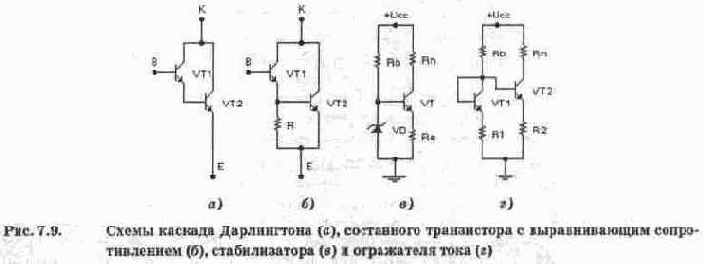
Идея стабилизатора тока на рис. 7.9, в заключается в стабилизации напряжения базы транзистора с помощью параметрического стабилизатора, состоящего из стабилитрона VD и последовательно включенного с ним балластного резистора Rb. Постоянство напряжения на базе обеспечивает постоянство напряжения на резисторе Re и однозначно связанный с коллекторным током ток эмиттера, протекающий через нагрузку Rn.
В аналоговых интегральных схемах широкое распространение получил стабилизатор тока под названием "токовое зеркало" или отражатель тока (рис. 7.9, в). Из сравнения схем на рис. 7.9, в, г нетрудно установить сходство между отражателем тока и простейшим стабилизатором. Отличие заключается в том, что в отражателе вместо стабилитрона используются резистор R1 и прямо смещенный р—п-переход, роль которого играет транзистор VT1, включенный по схеме диода.
Если сопротивления R1 и R2 сделать неодинаковыми, то неодинаковыми будут и токи эмиттеров. При этом ток в нагрузке равен
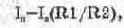
где I, — ток через резистор R1.
Как видно из выражения (7.14), ток 1„ может быть больше или меньше тока I, в зависимости от отношения R1/R2; обычно оно не превышает нескольких единиц из-за ограничений по площади, занимаемой на кристалле резисторами с большим сопротивлением.
Из (7.14) следует, что выходным током 1„ можно управлять, меняя тем или иным способом входной ток 1„ в чем и проявляется достоинство отражателя тока. Кроме того, в выражение (7.14) не входят ни напряжение на стабилитроне, ни коэффициент усиления тока. Это значит, что работа отражателя тока в первом приближении не зависит от изменения этих параметров, т.е. от изменений температуры прежде всего.
Чтобы обеспечить особо малые выходные токи (например, при работе ДУ в микрорежиме) сопротивление R1 делают равным нулю. Для такого варианта
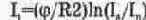
и зависимость тока нагрузки 1„ от тока управления I, значительно слабее, а управление выходным током менее эффективно.
Контрольные задания
1. Используя схему ДУ на рис. 7.7, исследуйте зависимость коэффициента усиления от параметров транзисторов VT1, VT2 (Re', Кь', <х) и степени неиндентичности внутренних сопротивлений источников входных сигналов. Результаты моделирования сравните с данными расчетов.
2. Выполните исследования по п. 1 для режима синфазного входного сигнала при двух значениях амплитуды входных сигналов, равной 0,lUcc и O.QUcc.
3. Для ДУ на рис. 7.7 исследуйте зависимость напряжения смещения от неидентичности коллекторных нагрузок (R1, R2) и цепей смещения (RIs, R2s), а также параметров транзисторов VT1 и VT2 (тепловой ток коллектора, коэффициент усиления по току и др.). При изменении параметров транзисторов необходимо в библиотеке компонентов сделать копию для одного из транзисторов ДУ с изменением названия, например, одному присвоить имя 1, а другому — 2.
4. В схеме ДУ на рис. 7.7 замените стабилизатор тока на транзисторе VT3 на отражатель тока (рис. 7.9, в), используя в качестве резистора Рь резистор R3 ДУ. При этом коллектор транзистора VT2 отражателя соедините с эмиттерами транзисторов ДУ. Подберите сопротивления эмиттерных резисторов отражателя таким образом, чтобы сохранился первоначальный статический режим. После таких изменений измерьте коэффициенты усиления для дифференциального и синфазного сигнала и полученные данные сравните с предыдущими результатами.
Каскодная схема.
Под каскодом понимается схема, в которой два транзистора соединены последовательно, так что через них в статическом режиме протекает один и тот же ток (рис. 7.10) (на практике находят применение и другие каскодные схемы, в частности, с параллельным питанием и последовательным соединением по переменному току, а также рассматриваемые ниже гибридные каскодные схемы). Транзистор VT1 ключен по схеме с ОЭ, а VT2 — по схеме с ОБ. Режим по постоянному току задается с помощью резисторов R1, R2, R3. Режим ОБ транзистора VT2 по переменной составляющей обеспечивается блокировочным конденсатором СЬ, подключенным к его базе. На рис. 7.10 показаны также необходимые для исследования контрольно-измерительные приборы.
Каскодная схема имеет коэффициент усиления тока а=а'a", где a', a" — коэффициенты усиления тока первого и второго транзисторов. Коэффициент усиления напряжения каскода определяется приближенной формулой
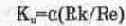
Как следует из (7.15), коэффициент усиления каскода по напряжению такой же, как и в простейшем каскаде ОЭ (это вытекает из того, что первый транзистор имеет К„=1). В данном случае он равен 5, что подтверждается и результатами осцил-лографических измерений, приведенных на рис. 7.11.
Не давая выигрыша по коэффициенту усиления напряжения и тока (а также по входному и выходному сопротивлениям), каскодная схема имеет важное преимущество, которое заключается в уменьшении паразитной связи между выходом Uo и входом Ui. В простом каскаде по схеме с ОЭ выход и вход связаны через емкость коллекторного перехода, что в ряде случаев осложняет работу усилителей. В частности, она приводит к увеличению входной емкости каскада, превращая каскад с ОЭ в своеобразный интегрирующий усилитель (в усилительной технике это называется эффектом Миллера), когда с ростом коэффициента усиления растет и входная емкость. При наличии индуктивной составляющей сопротивления нагрузки и при определенной реактивности выходного сопротивления предыдущего каскада такая связь часто приводит к самовозбуждению усилителя.

Рис. 7.10. Каскодная схема
Причина, по которой выход и вход в каскоде связаны в меньшей степени, заключается в том, что база VT2 находится под неизменным напряжением и его величину можно считать как бы напряжением питания для транзистора VT1, а его нагрузкой — весьма малое сопротивление эмиттерного перехода VT2 [12]. Это означает, что транзистор VT1 работает практически в режиме короткого замыкания коллекторной цепи. Соответственно его коэффициент усиления близок к единице, эффект Миллера отсутствует, и входная емкость равна емкости коллектора. Благодаря такой особенности каскод находит широкое применение в резонансных усилителях, в частности, в высокочастотных каскадах радиоприемных устройств.
Контрольные вопросы и задания
1. Какими достоинствами обладает каскодная схема?
2. В схеме рис. 7.10 при Rk=7,5 кОм установите статический режим в соответствии с показаниями приборов на рис. 7.10. В процессе моделирования измерьте коэффициент усиления напряжения и сравните полученные данные с результатами расчетов по формуле (7.15). Определите максимальный входной сигнал, при котором он передается на выход каскада без искажений. Изменяя параметры одного из транзисторов, исследуйте влияние асимметрии транзисторов по a, R,\ R¦,' на статический режим и коэффициент усиления напряжения.
3. Подготовьте схемы для моделирования гибридных каскодных схем на полевых и биполярных транзисторах [52] (рис. 7.12), подключив к ним источник питания, недостающие компоненты (см. рис. 7.4, 7.10) и необходимые контрольно-измерительные приборы. В процессе моделирования установите необходимый статический режим (из условия неискаженной передачи сигнала), определите коэффициент усиления напряжения и сравните его с данными расчетов по формулам: для каскодной схемы
для
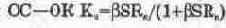
для
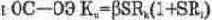
Выходные каскады
Задачей выходных каскадов является обеспечение заданной мощности в нагрузке. Коэффициент усиления напряжения является для выходных каскадов второстепенным параметром; -для них наиболее важными являются коэффициент полезного действия и коэффициент нелинейных искажений при обеспечении заданной мощности.
Выходные каскады обычно потребляют основную часть мощности усилителя, поэтому высокий КПД имеет существенное значение. Это особенно важно для интегральных схем, в которых мощность, рассеиваемая кристаллом, ограничена. Что касается коэффициента нелинейных искажений, то для выходных каскадов он имеет немаловажное значение, поскольку в таких каскадах усиливаемые сигналы максимальны.
Коэффициент полезного действия определяется как отношение выходной мощности каскада к мощности, отбираемой от источника питания Ucc: КПД=и„1„,/2и„1,р, где U„,, !„ — амплитуды выходного тока и напряжения; Icp — среднее значение потребляемого каскадом тока.
Коэффициент нелинейных искажений характеризует отличие формы выходного сигнала от формы входного, что обусловлено нелинейностью передаточной характеристики каскада. Нелинейные искажения характеризуются появлением в выходном сигнале новых гармоник, отсутствующих во входном сигнале. Характеристикой нелинейных искажений является отношение суммарной мощности высших гармоник, начиная со второй, к мощности первой гармоники (на частоте входного сигнала).
Допустимое значение коэффициента нелинейных искажений определяется конкретными требованиями к той или иной аппаратуре. Например, при воспроизведении звука в аппаратуре среднего качества допускаются искажения 2...3%, в измерительных устройствах и усилителях высокого класса его значения существенно меньше.
Как отмечалось выше, имеется несколько типов режимов работы выходных каскадов.
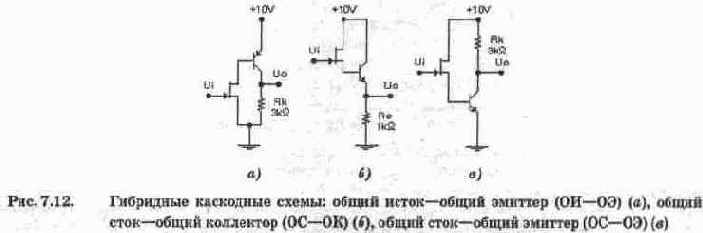
Класс А характеризуется минимальными нелинейными искажениями и малым КПД. Класс В характеризуется тем, что рабочая точка в режиме покоя расположена на границе квазилинейного участка, которая соответствует запертому состоянию транзистора. Очевидно, что в этом случае усиливаются только положительные полуволны входного сигнала. Поэтому выходное напряжение оказывается существенно несинусоидальным, т.е. содержит большое число гармоник. Анализ показывает, что коэффициент нелинейных искажений в классе В независимо от амплитуды сигнала составляет около 70%, что в большинстве случаях неприемлемо. Режим класса В реализуется в так называемой двухтактной схеме, состоящей по существу из двух усилителей, один из которых усиливает положительную полуволну сигнала, а другой — отрицательную. В нагрузке эти полуволны складываются и образуют полную синусоиду.
На рис. 7.13, а показана наиболее простая двухтактная схема класса В, выполненная на коплементарных транзисторах (транзисторах разной проводимости). Нагрузка Rn включена в эмиттерную цепь транзисторов, работающих в режиме повторителей напряжения. В режиме покоя оба транзистора заперты, поскольку напряжения на эмиттерных переходах равны нулю. Во время положительной полуволны входного сигнала Ui открывается транзистор VT1, а во время отрицательной полуволны — транзистор VT2. Коэффициент усиления мощности близок к отношению эмиттерного и базового токов, т.е. равен В+1.
При очевидной простоте схемы на рис. 7.13, а ей свойственны сравнительно большие нелинейные искажения, что связано с наличием так называемой "пятки" на входной ВАХ биполярных транзисторов. Очевидно, что такие искажения будут особенно существенны при малых входных сигналах с амплитудой, сравнимой с напряжением база—эмиттер в рабочей точке. Для устранения этого недостатка используют раздельные схемы подачи смещения на базы транзисторов (рис. 7.13, б), что обеспечивает режим класса АВ.
При построении выходного каскада на однотипных транзисторах используется схема на рис. 7.13, в. В ней транзистор VT2 открыт в течение обоих полупериодов. В режиме покоя ток транзистора выбирается так, чтобы потенциал коллектора VT2 был равен нулю. При этом диод VD и транзистор VT1 заперты; ток в нагрузке отсутствует. Во время положительной полуволны входного сигнала потенциал коллектора VT2 уменьшается, при этом открывается диод VD и через нагрузку начинает протекать ток. Транзистор VT1 остается закрытым, так как прямое напряжение Е на диоде создает на эмиттерном переходе обратное смещение. Во время отрицательной полуволны потенциал коллектора VT2 повышается, отпирается транзистор VT1 и через нагрузку протекает ток, обусловленный транзистором VT1. При этом диод заперт, так как прямое напряжение Е на эмиттерном переходе создает на диоде обратное смещение.
Для того чтобы открылся диод VD (при положительной полуволне) или транзистор VT1 (при отрицательной полуволне), потенциал коллектора VT2 должен измениться на величину ±Е (напряжение база—эмиттер в статическом режиме) по сравнению с потенциалом покоя. Следовательно, минимальная амплитуда входного сигнала, на которую реагирует рассматриваемый каскад, составляет Е/К, где К — коэффициент усиления каскада на транзисторе VT2. Для исследования каскада на рис. 7.13, в используется схема на рис. 7.14.
Рис. 7.14. Схема для исследования выходного каскада
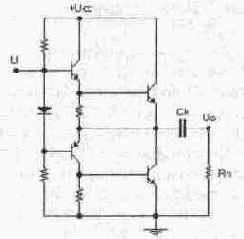
Рис. 7.15. Выходной двухтактный каскад с однополярным питанием
Возможны и другие схемы выполнения выходных каскадов, в том числе и с однополярным питанием. Одна из них приведена на рис. 7.15. Ее особенностью является то, что конденсатор Ск, включенный последовательно с нагрузкой Rn, после его зарядки до напряжения Е, равного напряжению на эмиттерах транзисторов в статическом режиме, работает в течение одного из полупериодов как источник питания.
В мощных выходных каскадах на базе эмиттерных повторителей короткое замыкание на выходе, как правило, приводит к выходу транзисторов из строя из-за превышения коллекторным током допустимого значения. Для защиты от коротких замыканий в эмиттерные цепи мощных выходных транзисторов включают небольшие ограничивающие ток сопротивления (несколько ом) или вводят дополнительные транзисторы, которые открываются только при больших токах нагрузки и, шунтируя входную цепь, ограничивают выходной ток на безопасном уровне. Одна из возможных схем защиты с помощью дополнительных транзисторов показана на рис. 7.16.
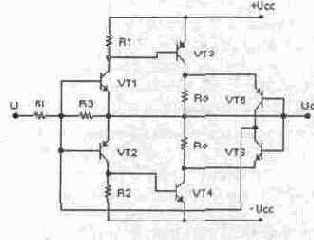
Рис. 7.16. Выходной каскад с защитой от коротких замыканий
Схема защиты работает следующим образом. При коротком замыкании в нагрузке ток через сопротивление Ro увеличивается и создает падение напряжения, открывающее в соответствующие полупериоды транзисторы VT5, VT6. Оказываясь в режиме насыщения, они шунтируют входную цепь мощного усилительного каскада. В итоге входное напряжение ограничивается сопротивлением Ri и токи транзисторов VT3, VT4 не превышают значений, при которых они работают в номинальном режиме. Подобная защита имеет высокое быстродействие и обеспечивает надежную работу мощных усилительных каскадов. При ее введении обязательно наличие дополнительного резистора Ri, сопротивление которого выбирается, исходя из минимально допустимого значения сопротивления нагрузки предварительного усилителя, к которому подключается выходной каскад.
Контрольное задание
1. Путем подбора сопротивления RI в схеме на рис. 7.14 установите зафиксированный приборами статический режим при R2=Rn=100 Ом. Определите коэффициент усиления каскада и максимальный входной сигнал, при котором он передается на выход без искажений (определяется визуально).
2. Составьте схему исследования выходного каскада (рис. 7.15) и проведите ее моделирование.
Многокаскадные усилители
При разработке многокаскадных усилителей очень важен выбор типа связи между отдельными усилительными каскадами. Обычно используется гальваническая (непосредственная), емкостная, трансформаторная и оптронная связь. Для низкочастотных усилителей чаще всего используют два первых типа связи. Третий тип применяют значительно реже из-за больших габаритов трансформаторов и их высокой стоимости (трансформаторная связь может быть успешно использована для получения максимального усиления мощности при достаточно высоком КПД). Оптронная связь между каскадами применяется сравнительно редко, только в специальных случаях, когда при низкой рабочей частоте требуется хорошая гальваническая развязка между каскадами.
При проектировании многокаскадных усилителей, к которым не предъявляются специальные требования, обычно задают выходную мощность и напряжение, сопротивление нагрузки, допустимый коэффициент гармоник, рабочий диапазон частот, входное напряжение, внутреннее сопротивление источника питания и другие параметры.
При разработке усилительных устройств предусматриваются средства, обеспечивающие защиту его входных цепей от возможных перегрузок при случайном воздействии помех большого уровня, приводящих в лучшем случае к перегрузке усилителя и кратковременной потере его работоспособности. Чаще всего для этого на входе усилителя используется диодный ограничитель (см. гл. 8).
Наиболее ярким примером многокаскадных усилителей являются операционные усилители (ОУ). Их отличие от усилителей, выполненных на дискретных элементах, заключается в основном только в методах изготовления отдельных компонентов схем и технологии изготовления законченных функциональных узлов. Однако в большинстве случаев принципиальные схемы интегральных усилителей выглядят значительно сложнее своих дискретных аналогов. Это объясняется тем, что введение нескольких транзисторов в схему усилителя для незначительного улучшения каких-либо его параметров при интегральной технологии не вызывает затруднений и не оказывает существенного влияния на его стоимость.
Благодаря использованию двухполярного питания ОУ обладает замечательной особенностью, которая позволяет получить близкое к нулю выходное напряжение при отсутствии входного сигнала. Это свойство позволяют подключать к ОУ нагрузку и источники входных напряжений, не заботясь о разделении переменной и постоянной составляющей сигнала.
В составе ОУ как многокаскадного усилителя условно можно выделить входную, выходную части и каскады связи между ними.
Входная часть ОУ содержит дифференциальные усилители. Выходная часть включает каскады усиления мощности и обеспечивает работу ОУ на заданную нагрузку. Каскады связи служат для усиления по напряжению и позволяют осуществить согласование уровней сигнала.
В зависимости от количества каскадов, вносящих основной вклад в получение требуемого коэффициента усиления напряжения, ОУ условно делят на двух- и трехкаскадные. Как правило, предпочтение отдается двухкаскадным ОУ. Они имеют лучшую стабильность параметров, могут работать при значительных изменениях напряжения питания, более экономичны. Для коррекции частотной характеристики в двухкаскадных ОУ используется минимальное количество внешних элементов (необходим лишь один конденсатор малой емкости). Кроме того, в них легко осуществляется регулировка уровня выходного напряжения (установка нуля) с помощью одного потенциометра балансировки.
В многокаскадных усилителях на базу каждого следующего каскада поступает не только полезный сигнал, но и постоянная составляющая напряжения с коллектора предыдущего каскада. Для согласования по постоянной составляющей на входе каждого каскада используются так называемые схемы сдвига уровня.
Простейшей схемой сдвига уровня является эмиттерный повторитель, у которого уровень выходного потенциала (потенциала эмиттера) ниже уровня потенциала базы на величину Е (напряжение эмиттер—база в статическом режиме), а сигнал передается с коэффициентом передачи К=1.
Одна из возможных схем, иллюстрирующая принцип сдвиг уровня с использованием эмиттерного повторителя, показана на рис. 7.17, а. Транзистор VT1, на базу которого подается входной сигнал Ui, выполняет роль эмиттерного повторителя. Транзистор VT2 включен генератором тока, на его базу подается напряжение Us от специальной цепи смещения. Уровень выходного напряжения определяется напряжением Е и падением напряжения на резисторе R1
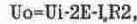
где ток I, — ток, задаваемый стабилизатором на транзисторе VT2; умножение Е на 2 связано с тем, что в процессе формирования уровня сдвига участвуют двар—п- перехода — транзисторов VT1 и VT3.
Коэффициент передачи по переменной составляющей определяется внутренним сопротивлением стабилизатора тока, которое значительно больше сопротивления резистора R2.
На рис. 7.17,6 показана еще одна схема сдвига уровня, которая отличается наличием дополнительного диода VD, обеспечивающего дополнительный сдвиг напряжения на величину Е. Резистор R1 служит для точной подгонки необходимого уровня сдвига. Достоинством этой схемы является возможность получения любого уровня сдвига за счет использования N включенных последовательно диодов, при этом выражение (7.16) может быть записано в следующем виде: Uo=Ui-(N+2)E-I,Rl.
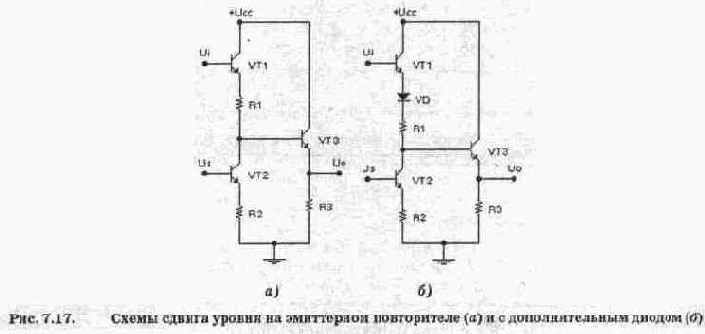
В качестве примера применения рассмотренных в этой главе отдельных элементов на рис. 7.18 показана схема одного из первых отечественных ОУ серии 140УД1.
Первый каскад ОУ 140УД1состоит из ДУ на транзисторах VT1, VT2 с генератором тока в цепи эмиттера на транзисторе VT3. Температурная стабилизация тока осуществляется транзистором VT4. Второй каскад на транзисторах VT5 и VT6 гальванически связан с выходами первого. На выходе усилителя включены два эмиттерных повторителя на транзисторах VT7 и VT9. Каскад на транзисторе VT8 осуществляет сдвиг уровня постоянного напряжения.
Операционные усилители этой серии выпускаются двух типов, рассчитанных на различные питающие напряжения: К140УД1А — на 6,3 В (Р„,=45 мВт) и К140УД1Б — на 12,6 В (Р„„=170 мВт).
Подключение корректирующих элементов осуществляется между контактами 1 и 12 или 9 и 12 в зависимости от условий применения. Выбор емкости корректирующей емкости зависит от реализуемого усиления, при этом ОУ обладает различной полосой пропускания. Минимальное сопротивление нагрузки усилителя Rn=5 кОм.
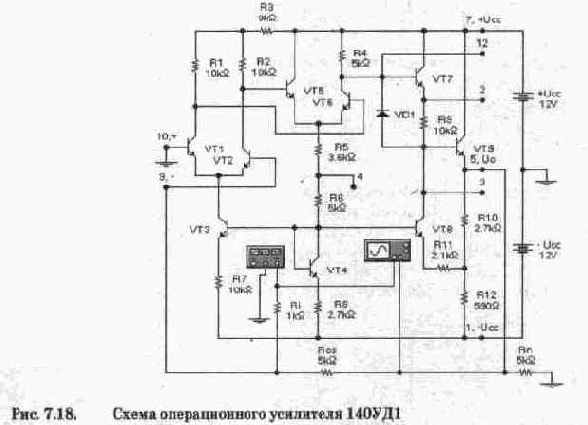
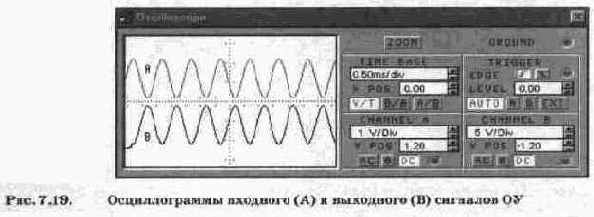
На схеме рис. 7.18 ОУ включен по схеме инвертирующего усилителя без каких-либо элементов коррекции (в данном случае использованы транзисторы типа Ideal). Коэффициент усиления напряжения равен Ku=Ros/Ri=5, что подтверждается осциллографическими измерениями, результаты которых приведены на рис. 7.19.
Контрольные вопросы и задания
1. Что такое схема сдвига уровня, в усилителях какого типа она используется?
2. По какой схеме выполнен выходной каскад ОУ на рис. 7.18?
3. Рассчитайте коэффициент усиления схемы на рис. 7.18 при Ros=l и 10 кОм. Результаты расчета проверьте моделированием.
4. При моделировании схемы на рис. 7.18 поменяйте по очереди все транзисторы, начиная с выходного каскада, на транзисторы типа 2N222 из библиотеки 2п, проверяя после каждой замены работоспособность схемы. Напомним, что отмена введенных изменений производится командой Revent to Saved из меню File.
Транзисторные усилительные схемы
В данной главе рассматриваются базовые схемы усилителей на биполярных и полевых транзисторах, согласующие устройства многокаскадных усилителей, а также их выходные каскады. В конце главы в качестве примера использования рассмотренных элементов приведена схема одного из первых операционных усилителей в интегральном исполнении.
7.1. Базовые усилительные каскады
7.2. Дифференциальный усилитель
7.3. Каскодная схема
7.4. Выходные каскады
7.5. Многокаскадные усилители
Генераторы гармонических колебаний
Генераторы гармонических колебаний представляют собой устройства из частотно-избирательной цепи и активного элемента. По типу частотно-избирательной цепи они делятся на LC- и RC-генераторы.
Генераторы LC-типа имеют сравнительно высокую стабильность частоты колебаний, устойчиво работают при значительных изменениях параметров транзисторов, обеспечивают получение колебаний, имеющих малый коэффициент гармоник. В генераторах LC-типа форма выходного напряжения весьма близка к гармонической. Это обусловлено достаточно хорошими фильтрующими свойствами колебательного контура. К недостаткам LC-генераторов относятся трудности изготовления высоко-стабильных температурно-независимых катушек индуктивности, а также высокая стоимость и громоздкость последних. Это особенно проявляется при создании низкочастотных автогенераторов, в которых даже при применении ферромагнитных сердечников габаритные размеры, масса и стоимость получаются значительными.
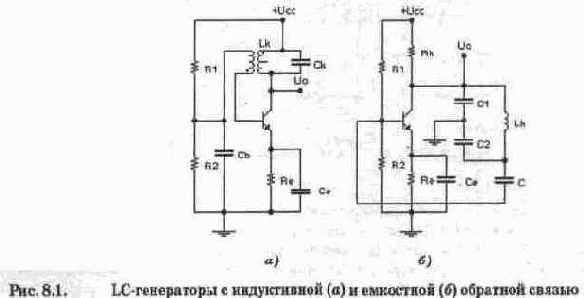
Базовые схемы LC-генераторов показаны на рис. 8.1 [53]. Схему на рис. 8.1, a называют индуктивной трехточкой или схемой Хартлея, на рис. 8.1,6 — емкостной трехточкой или схемой Колпитца. Для обеих схем с помощью резисторов Rl, R2 и Re устанавливается необходимый режим по постоянному току. Конденсаторы СЬ и Се — блокировочные, конденсатор С называют конденсатором связи. Частота автоколебаний для обеих схем в первом приближении определяется известной формулой
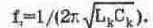
Для схемы Колпитца
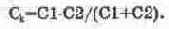
Для всех автогенераторов условиями возникновения автоколебаний является наличие положительной обратной связи при коэффициенте усиления равном или большим 1. Для схемы Хартлея эти условия обеспечиваются за счет транзисторного каскада, выбора коэффициента трансформации и соответствующего включения обмотки связи. Положительная обратная связь в генераторе Колпитца обеспечивается за счет того, что сигнал обратной связи поступает с такого зажима колебательного контура, при котором сигнал обратной связи на базе транзистора совпадает по фазе с переменным сигналом на коллекторе. Коэффициент передачи цепи обратной связи при этом определяется коэффициентом передачи емкостного делителя, образованного конденсаторами С1 и С2. При выполнении указанных условий устройство самовозбуждается. Процесс самовозбуждения происходит следующим образом. При включении источника питания конденсатор колебательного контура, включенного в коллекторную цепь, заряжается. В контуре возникают затухающие колебания, которые одновременно передаются на управляющие электроды транзистора по цепи положительной обратной связи. Это приводит к пополнению энергией LC-контура и колебания превращаются в незатухающие.
Выполним моделирование автогенератора Колпитца (рис. 8.2), схема которого заимствована из каталога программы EWB 4.1 (схемный файл 2m-oscil.ca4). В отличие от базовой схемы (рис. 8.1, б) она выполнена на эмиттерном повторителе.
Рис. 8.2. Генератор Колпитца
Расчеты по формулам (8.1) и (8.2) для схемы на рис. 8.2 дают: С2=1мкФ;
Из осциллограмм на рис. 8.3 видно, что результаты моделирования крайне неутешительны. Во-первых, период колебаний, отсчитывемый с помощью визирных линеек и равный Т2-Т1=7,34 мс, заметно больше теоретического — 6,28 мс. Во-вторых, форма колебаний далеко не синусоидальная. Такие результаты можно объяснить слишком сильной связью колебательного контура с усилительным каскадом. В пользу этого утверждения свидетельствует и тот факт, что двойная амплитуда выходного сигнала практически равна напряжению источника питания 6 В. Для возможности управления взаимодействием колебательного контура с транзисторным каскадом введем конденсатор связи С (рис. 8.4).
Результаты моделирования схемы на рис. 8.4 приведены на рис. 8.5, из которого видно, что форма колебаний существенно улучшилась и действительно стала синусоидальной. При этом период колебаний 6,144 мс практически равен теоретическому значению.
Из проведенных экспериментов видно, насколько велика роль правильного выбора взаимодействия колебательного контура со снабжающим его энергией усилительно-согласующим устройством. В технической литературе для этого введен термин "коэффициент регенерации". Этот безразмерный коэффициент показывает, во сколько раз может быть уменьшена добротность колебательной системы по сравнению с ее исходным значением (за счет вносимых по цепи обратной связи потерь), чтобы автогенератор оказался на границе срыва колебаний. Для низкочастотных генераторов этот коэффициент выбирают равным 1,5... 3.
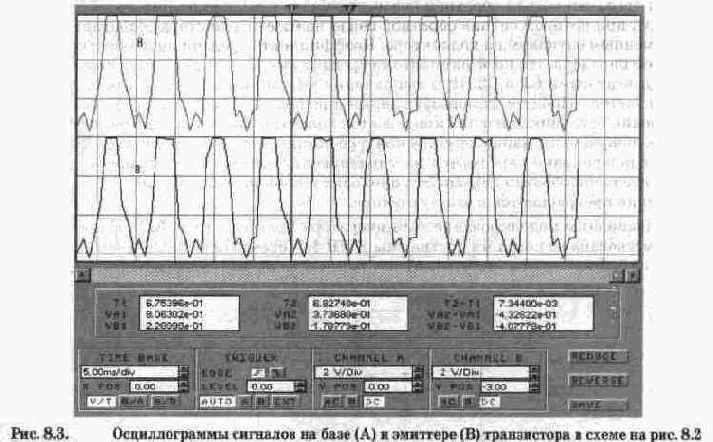
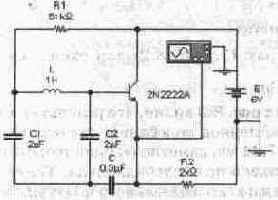
Рис. 8.4. Генератор Колпитца с конденсатором связи
Особо следует сказать о блокировочных конденсаторах СЬ и Се в базовой и эмиттерной цепях. При достаточно глубокой обратной связи и неправильно подобранных емкостях этих конденсаторов может возникать прерывистая генерация или автомодуляция. В этом случае амплитуда колебаний будет иметь переменное значение или уменьшаться до нуля. Прерывистая генерация обусловлена тем, что при определенных условиях напряжение автоматического смещения вследствие заряда конденсаторов СЬ и Се может приблизиться к амплитуде напряжения обратной связи, за счет чего транзистор запирается и колебательный контур перестанет пополняться энергией. В итоге автоколебания быстро затухнут и возникнут снова только после разряда этих конденсаторов. Затем процесс нарастания амплитуды, заряда конденсаторов и срыва автоколебаний повторится. Поэтому цепи, обеспечивающие автоматическое смещение, приходится, как правило, подбирать при настройке.
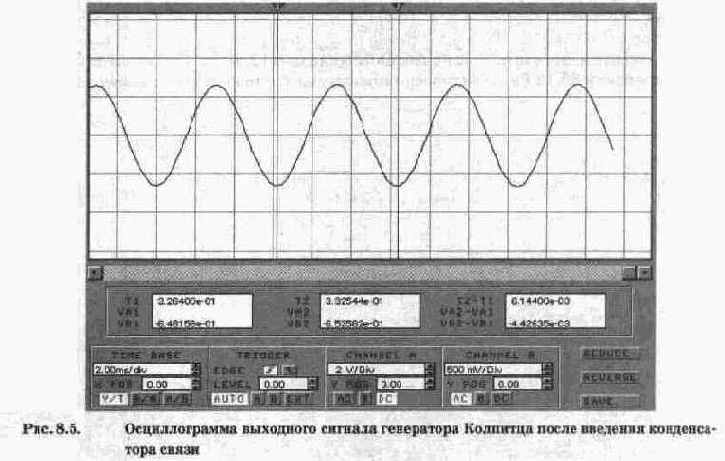
Перестройку частоты LC- генераторов обычно осуществляют изменением емкости конденсатора колебательного контура. При этом изменяется и добротность контура из-за изменения соотношения L/C, что может вызвать изменение режима работы автогенератора. Изменение емкости обычно производят механическим путем или с помощью варикапа, изменяя напряжение смещения.
На практике находят применение также LC-генераторы с использованием элементов с отрицательным сопротивлением. В качестве примера рассмотрим схему такого генератора, показанную на рис. 8.6 [30]. Он содержит эмиттерный повторитель на транзисторе VT1, который предназначен для регулировки выходного напряжения генератора путем изменения напряжения на его базе с помощью резисторов R1 и R2. Собственно генератор состоит из колебательного контура Lk, Ck и двух полевых транзисторов VT2 и VT3 с каналами разной проводимости, которые обладают участком с отрицательным дифференциальным сопротивлением. Приведенная в [30] вольтамперная характеристика такого гибрида на отечественных полевых транзисторах КПЗОЗ и КП103 имеет форму несимметричного колоколообразного импульса с вершиной при напряжении 3 В (ток 2 мА) и практически нулевым током при напряжении 8 В. Следовательно, после включения питания, когда напряжение на конденсаторе Ск достигает 3 В, начинается резкое увеличение шунтирующего этот конденсатор сопротивления, в результате чего увеличивается скорость заряда конденсатора. Во второй фазе, когда при разряде конденсатора напряжение на нем достигает 8 В, скорость его разряда увеличивается и после достижения значения 3 В начинается форсированный разряд. Таким образом, колебательный контур в результате получает как бы два толчка в течение каждого периода колебаний, что приводит в конечном итоге к возникновению незатухающих колебаний.
Частота колебаний генератора на рис. 8.6 в первом приближении определяется
выражением (8.1) и составляет
Посмотрим, насколько это соответствует результатам моделирования, представленным на рис. 8.7. Из осциллограммы видно, что период колебаний составляет 12,48 мс, что соответствует частоте колебаний 80,12 Гц, практически совпадающей с теоретическим значением.
Рис. 8.6. Схема низкочастотного LC-генератора
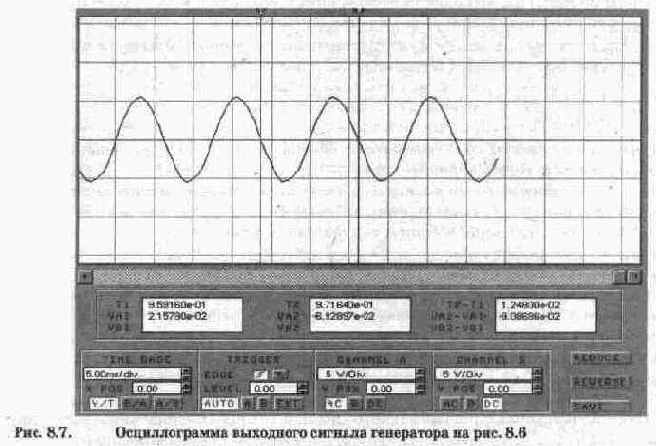
Перейдем к рассмотрению RC-генераторов. Генераторы такого типа достаточно просты в реализации, дешевы, имеют малые габариты и массу. Однако стабильность частоты колебаний в них значительно ниже, чем в LC-генераторах. Форма колебаний несколько отличается от синусоидальной и существенно изменяется в зависимости от значений параметров активного элемента и цепи обратной связи. Эти недостатки не позволяют применять их в схемах, где необходимо получать высокую точность и стабильность частоты колебаний, а также удовлетворительную форму выходного напряжения. В устройствах, где к этим параметрам не предъявляются жесткие требования, низкочастотные RC-генераторы используются достаточно широко.
В RC-генераторах обратная связь осуществляется за счет RC-цепей, обладающих избирательными свойствами и обеспечивающих на одной определенной частоте выполнение условий возбуждения колебаний. В этих генераторах выходное напряжение практически повторяет форму коллекторного тока транзистора. Поэтому они не могут работать с отсечкой тока и имеют сравнительно низкий КПД.
Избирательным ЕС-цепям присуща невысокая добротность. Поэтому для получения синусоидальных колебаний с малым уровнем гармоник приходится вводить неглубокую обратную связь. При этом активный элемент должен иметь небольшую нелинейность, чтобы в момент возникновения автоколебаний коэффициент усиления оставался больше единицы и тем самым при любых изменениях параметров схемы обеспечивались условия самовозбуждения.
RC-автогенераторы выполняют на основе однокаскадных и многокаскадных усилителей. В однокаскадных автогенераторах выход усилителя соединяется со входом через RC-цепи, обеспечивающие фазовый сдвиг 180° на рабочей частоте. Такие генераторы обычно выполняют на фиксированную частоту, их иногда называют цепочечными RC-генераторами.
В автогенераторах, выполненных на основе многокаскадных усилителей, применяют как усилители переменного тока, так и усилители постоянного тока на ОУ.
При использовании усилителей переменного тока число каскадов выбирают четным (обычно используют двухкаскадные усилители). Такой усилитель вносит близкий к нулю фазовый сдвиг между входным и выходным сигналами, поэтому цепь обратной связи, соединяющая выход со входом, должна обеспечивать на частоте автоколебаний нулевой фазовый сдвиг. Обычно в таких генераторах в качестве цепей обратной связи используют частото-избирательные мостовые схемы, допускающие перестройку частоты в достаточно широких пределах.
Цепочечные автогенераторы должны иметь цепь обратной связи,обеспечивающую фазовый сдвиг 180° на частоте автоколебаний. Для получения такого сдвига требуется не менее трех RC-цепей. Действительно, каждое RC-звено в самых идеальных условиях обеспечивает фазовый сдвиг на угол, меньший 90°; следовательно, два звена дают фазовый сдвиг, меньший 180°. На рис. 8.8, а приведена схема цепочечного генератора, выполненного на четырехзвенной RC-цепи и транзисторном каскаде ОЭ. Согласно [30] частота колебаний генератора на рис. 8.8, а определяется по формуле:
Обратимся теперь к результатам моделирования, представленным на рис. 8.8, б, откуда видно, что период колебаний выходного сигнала составляет 315 мс, что существенно отличается от расчетного значения (T=l/f„=461,5 мс). В связи с этим уместно заметить, что аналитические выражения для частоты колебаний RC-генераторов имеют весьма ориентировочный характер. Приведем два примера. Для расчета частоты колебаний используем две разные формулы для RC-генератора с трехзвенной фазосдвигаю-щей цепью из работ [48, 53], с помощью которых для схемы на рис. 8.8, а получим:
Из приведенных результатов видно, что для рассматриваемой схемы более подходит результат, полученный с помощью формулы (8.4) из работы [48]. Проведем дополнительные испытания модели с трехзвенной цепочкой на рис. 8.9,а. Из приведенных на рис. 8.9, б результатов испытаний видно, что период колебаний RC-генерато-ра с трехзвенной цепочкой (515 мс) является чуть ли не средним арифметическим между результатами, полученными по формулам (8.3) и (8.5). Таким образом, и в этом случае имеются существенные расхождения результатов моделирования и расчета, причем более существенными являются расхождения между расчетными значениями с использованием различных расчетных соотношений для одной и той же схемы. Это позволяет сделать вывод, что аналитические выражения для RC-генерато-ров имеют очень приближенный (действительно, ориентировочный) характер.
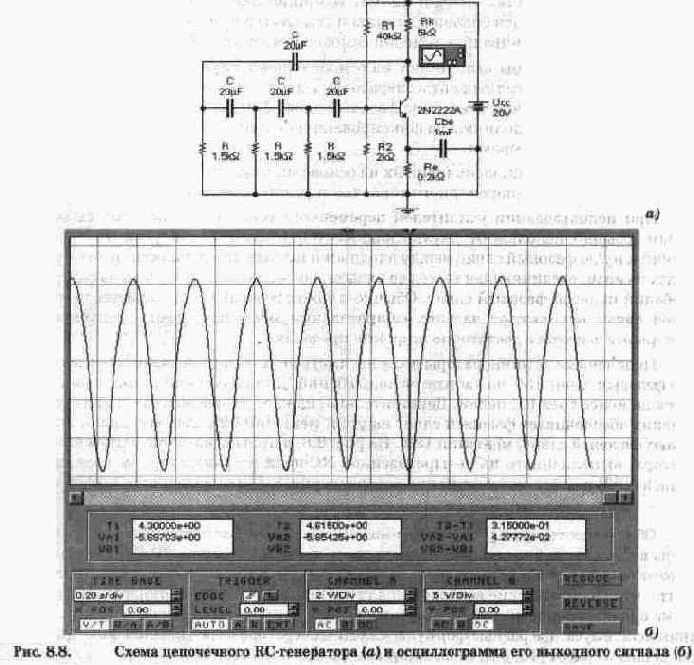
Контрольные вопросы и задания
1. При каких условиях усилительное устройство, охваченное обратной связью, может превратиться в автогенератор?
2. Для схемы генератора на рис. 8.2 установите путем моделирования зависимость формы генерируемого сигнала от соотношения емкости конденсаторов С1 и С2. При варьировании емкостей этих конденсаторов обеспечьте постоянство частоты колебаний, т.е. эквивалентной емкости контура С„.
3. В схеме генератора на рис. 8.4 путем изменения емкости конденсатора связи С установите граничные условия надежного самовозбуждения генератора без ухудшения формы генерируемых сигналов (определяется визуально).
4. Исследуйте в генераторе на рис. 8.6 влияние на форму сигнала, его амплитуду и частоту напряжения на базе транзистора (устанавливается изменением сопротивления резисторов Rl, R2) и емкости блокировочного конденсатора Се.
5. Используя материалы гл. 4, получите вольтамперную характеристику применяемого в схеме на рис. 8.6 гибридного компонента на моделях полевых транзисторов типа Ideal.
6. Исследуйте зависимость формы сигнала, частоты колебаний и надежности запуска RC-генератора на рис. 8.8 и 8.9 от напряжения питания Ucc.
Устройства на полупроводниковых приборах
В данной главе рассмотрены устройства для генерации, формирования, селекции и ограничения сигналов, а также транзисторные ключи для цифровых и аналоговых сигналов.
8.1. Генераторы гармонических колебаний
8.2. Транзисторные ключи
8.3. Ограничители и фиксаторы уровня
8.4. Преобразователи формы сигналов
8,5. Генераторы пилообразного напряжения
8.6. Селекторы импульсов
8.7. Генератор с кварцевым резонатором
Часть II. Расчет и моделирование электронных схем
5. Цепи постоянного тока
6. Цепи переменного тока
7. Транзисторные усилительные схемы
8. Устройства на полупроводниковых приборах
9. Цифровые устройства
10. Аналоговые устройства на операционных усилителях
11. Аналогo-цифровые и цифро-аналоговые преобразователи
12. Источники электропитания
13. Элементы приемо-передающих устройств
14. Элементы устройств автоматики
15. Программа EWB Layout
